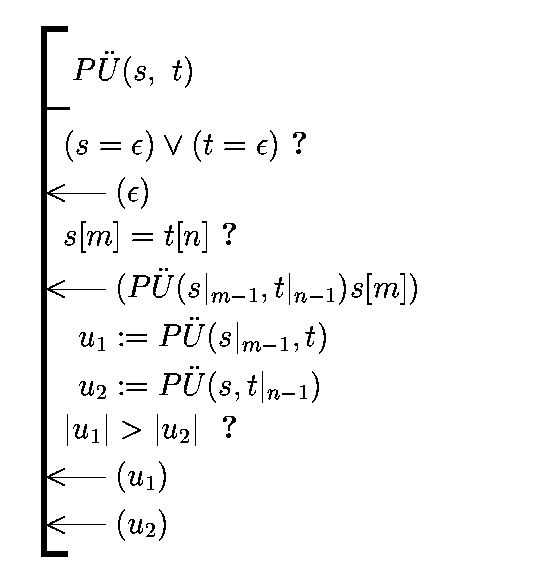Encoding objectives: compression, error correcting, cryptology, ... Coding scheme: alphabet-based coding scheme (vs dictionary based or block encoding), single-valued (unique) coding scheme (vs lossy). Prefixcode, 0-1 prefixcode. Code tree for a prefix code. Compression using variable length code. Huffman code and Huffman algorithm (greedy). Encoding (compressing) and decoding (decompressing) using Huffman codes. Other methods for compression. Shannon-Fano method.

Dynamic programming. Fibonacci sequence. Longest common subsequence problem.

Coding scheme is a mapping from source text to coded text.

Alphabet-based coding scheme maps each symbol separately - symbols have codes.

If the source text is uniquely retrievable from the coded text, then the coding scheme is called single valued (unique).

Single-valued coding scheme does not cause data loss. Multimedia coding schemes are often lossy (e.g. mp3).

Single-valued  alphabet-based coding scheme has the following properties:

Example of such a scheme is a prefix code: any code is not a prefix of any other code.

Let us have a look at binary code (0-1).
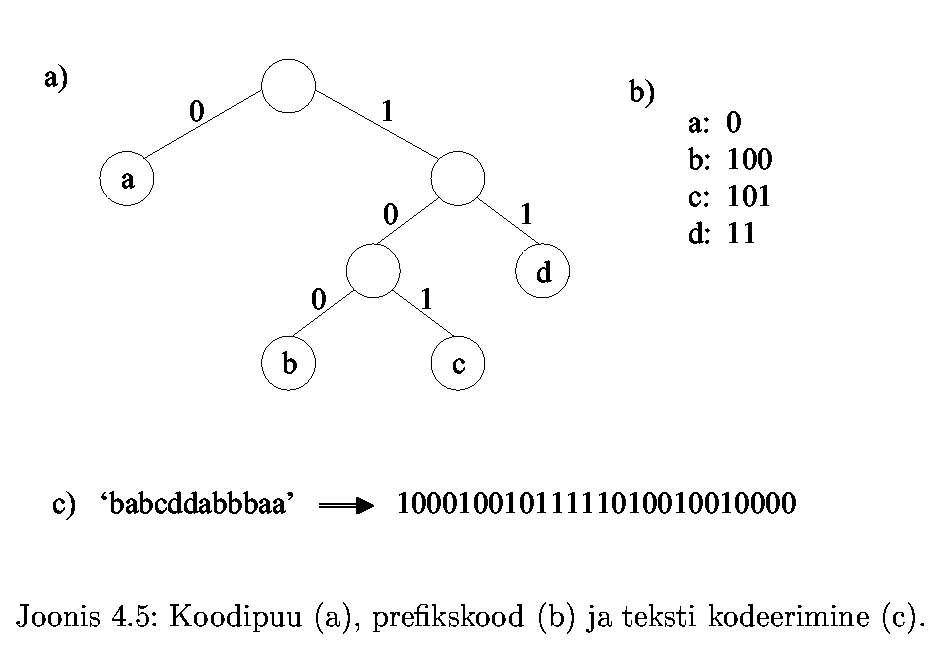
Prefix code to produce the binary code (0-1 prefix code) can be expressed as a binary tree: moving to left subtree adds 0 to the code, moving to right subtree adds 1 to the code, leaves contain symbols, coding starts from the root node.

This code tree represents a prefix code, because:

• different symbols reside in different leaves of the code tree, path from root to leaf is unique for each symbol
• no code can be prefix of any other code, because all true prefixes reside in intermediate (inner) nodes of the code tree

Example: ASCII-7 code tree is a perfect binary tree with 7 levels (each symbol has a different 7-bit code).

Idea: variable code length allows text compressing, if we give to frequent symbols shorter codes and to less frequent symbols longer codes.
To implement such a coding scheme we need to know the frequencies of the symbols.

In terms of 0-1 prefix code tree the frequent symbols must be closer to the root node, less frequent symbols can be deeper:




Huffman coding tree provides the optimal prefix code for a given text (no other coding is shorter).

Huffman coding tree is constructed using the following algorithm:

1. Pre-processing: find all different symbols in the text and for each symbol its frequency. We can skip pre-processing and use some language based estimate, but then the optimality is not guaranteed.
2. Build the leaves of the Huffman tree: for all different symbols store the symbol and its frequency in the leaf node. Add all leaves to some dynamic priority queue, that holds root nodes of tree fragments. Each root node contains frequency (sum of frequences of leaves in that fragment).
3. While there are at least two nodes in the queue:
1. choose and remove a node with smallest frequency from the queue
2. choose and remove another node with smallest frequency
3. build a new local root node and add removed nodes as children to this root node
4. add frequences of children and store the sum as frequency of the root node
5. add root node to the queue
4. If only one root remains in the queue, remove it and return as the root of the Huffman tree.

This is an example of a greedy algorithm: globally optimal result is achieved using "greedy" local choices.

   Huffman (byte[] original) {

      // initialization of leaves - there are 256 possible bytes
      leaves = new Node [256];
      for (int i=0; i<256; i++) {
         leaves [i] = new Node();
         leaves [i].left = null;
         leaves [i].right = null;
         leaves [i].symbol = (byte)(i-128); // Java specifics - signed bytes
         leaves [i].frequency = 0;
      }

      // calculate frequencies
      if (original.length == 0) {
         root = null;
         return;
      }
      for (int i=0; i<original.length; i++) {
         byte b = original [i];
         leaves [b+128].frequency++;
      }

      // build the tree
      LinkedList<Node> roots = new LinkedList<Node>();
      for (int i=0; i < 256; i++) {
         if (leaves[i].frequency > 0)
            roots.add (leaves[i]); // initial fragments
      } // for i
      while (roots.size()>1) {
         Node least1 = removeSmallest (roots);
         Node least2 = removeSmallest (roots);
         Node newroot = new Node();
         newroot.left = least1;
         newroot.right = least2;
         newroot.frequency = least1.frequency + least2.frequency;
         roots.addLast (newroot);
      }
      root = (Node)roots.remove (0);

      // Calculate the codes ...
   }


There are other compressing methods: e.g. replace repeating sequences by pair <number, sequence>, in case of two levels it is sufficient to store numbers only.  
1111111000111100000000000011111111: 7,3,4,12,8

Shannon-Fano method: bisection of symbol sets

Ziv-Lempel method is adaptive - coding scheme is vocabulary based and it is created dynamically during processing the source text.

Lossy compression - multimedia.
Steganography.

Subsequence of a string of length n is any string that is composed from remaining parts of the string after leaving out some (from 0 to n) symbols. There are  2ⁿ different subsequences in the worst case (when all symbols in the string are different). Empty string and the original string itself are also considered to be subsequences.

Example: "ABCD" has 16 subsequences:
empty, A, B, C, D, AB, AC, AD, BC, BD, CD, ABC, ABD, ACD, BCD, ABCD

Let us have two strings: s of length m and t of length n. Find a string u of length k such, that u is a subsequence for both strings s and t (common subsequence)  and k is maximal (from all possibilities). String u is not uniquely defined (sometimes there are many longest common subsequences), but the length k is unique.

Notice the following:

1. If s = s'X and t=t'X end on the same symbol X, u also has to end on this symbol (otherwise u is not the longest, because we can make it longer by adding symbol X to the end). We can now reduce the problem to shorter strings (where the last symbol is removed) s' and t' and append X to the solution of the shorter problem.
   
2. If s = s"Y and t=t"Z end on different symbols Y and Z, we have two possibilities to reduce the task to a simpler case:

• solve the problem for strings s and t"  (maybe t" ends on Y and we can use step 1, but there is no problem if we cannot make lcs longer - we can still use this reduction)
• solve the problem for stings s" and t (maybe s" ends on Z ...)
• choose, which of these two is longer

Worst case is the empty sequence (nothing in common, k=0), best case is s=t=u (k=m=n).

The following (extremely unefficient) recursive algorithm finds a solution:




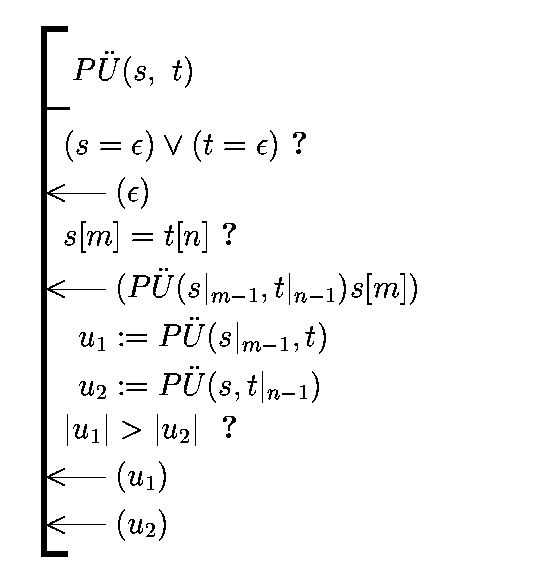We can remove the inefficiency if we use dynamic programming - method to construct a solution to the problem from (already stored) solutions to smaller problems.

We have seen this technique when we calculated Fibonacci numbers:
f(0)=0
f(1)=1
f(n)=f(n-2)+f(n-1)

For longest common subsequence problem we use two matrices: one keeps track on solutions of smaller problems (lengths) and other is used to memorize the way the solution was calculated. Time complexity to calculate these tables is O(m*n).


/** Finding the longest common subsequence (LCS) of two strings.
 * @author Jaanus
 */
public class Subsequence {

   /* source data */
   public static String s, t;
   public static int m, n;
   public static int[][] c, b;
   public static String lcs;

   /** Main method. */
   public static void main (String[] args) {
      if (args.length > 1) {
         s = args[0];
         t = args[1];
      } else {
         s = "yywzxyx";
         t = "xxyzywxy";
      }
      m = s.length();
      n = t.length();
      c = new int[m+1][n+1];
      b = new int[m+1][n+1];
      System.out.println ("s = " + s);
      System.out.println ("t = " + t);
      program();
      System.out.println();
      System.out.print ("          ");
      for (int j=0; j < t.length(); j++)
         System.out.print (t.charAt (j) + "    ");
      for (int i=0; i < c.length; i++) {
         System.out.println();
         if (i > 0)
            System.out.print (s.charAt(i-1) + "   ");
         else
            System.out.print ("    ");
         for (int j=0; j < c[i].length; j++) {
            System.out.print (c[i][j] + ";" + b[i][j] + "  ");
         }
      }
      System.out.println();
      int answer = c[m][n];
      System.out.println ("Answer: " + answer);
      for (int i=0; i <= m; i++) {
         for (int j=0; j <= n; j++) {
            if (c[i][j]==answer && b[i][j]==1) {
               findSolution (i, j);
               System.out.println (lcs);
            }
         }
      }
   }

   /** Dynamic Programming. */
   public static void program() {
      for (int i=0; i < c.length; i++) c[i][0] = 0;
      for (int j=0; j < c[0].length; j++) c[0][j] = 0;
      for (int i=1; i < c.length; i++) {
         for (int j=1; j < c[0].length; j++) {
            if (s.charAt(i-1) == t.charAt(j-1)) {
               c[i][j] = c[i-1][j-1] + 1;
               b[i][j] = 1; // increase lcs
            } else {
               if (c[i-1][j] > c[i][j-1]) {
                  c[i][j] = c[i-1][j];
                  b[i][j] = 2; // same column
               } else {
                  c[i][j] = c[i][j-1];
                  b[i][j] = 3; // same row
               }
            }
         }
      }
   }

   /** Read the solution from the table position i, j */
   public static void findSolution (int i, int j) {
      StringBuffer sb = new StringBuffer();
      while (i > 0 && j > 0) {
         if (b[i][j] == 1) {
            i--; j--;
            if (s.charAt (i) != t.charAt (j))
               throw new RuntimeException ("Error " + s + "  " + t);
            sb.append (s.charAt(i));
         } else {
            if (b[i][j] == 2) {
               i--;
            } else {
               if (b[i][j] == 3) {
                  j--;
               } else {
                  throw new RuntimeException ("Error " + s + "  " + t);
               }
            }
         }
      }
      lcs = sb.reverse().toString();
   }
}





Code

Jaanus Pöial