Programming techniques - recursion, exhaustive search

Programming Techniques

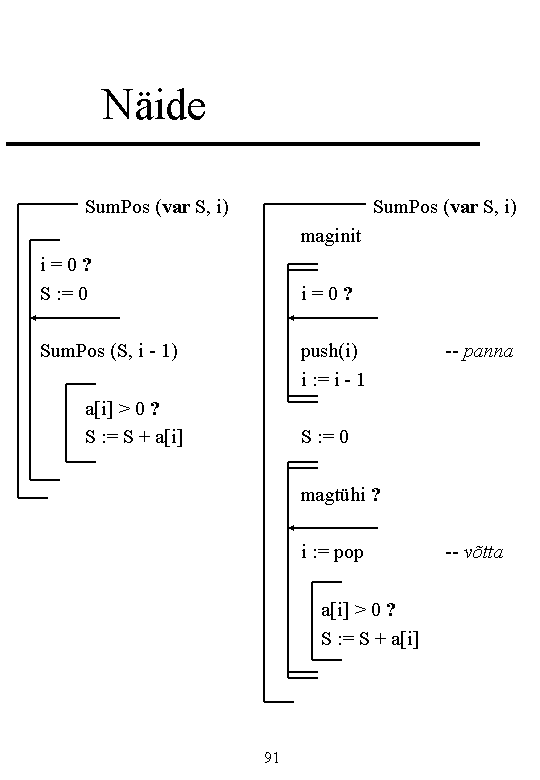
Recursion

Recursive algorithm calls itself for some "simpler" case.

Usually there are some "base case" and "inductive step" - like in mathematical induction.

Forms of recursion:

• direct:   A ->  A
• indirect:  A  ->  B  ->  ...  ->  A

Example. Factorial:

0! = 1
n! = n(n-1)!     if  n>0

Recursive definition does not imply a recursive program - usually simple loop is more effective.

Using the stack we can convert recursion to loop and loop to recursion.

Example. Fibonacci numbers (very ineffective recursive program, but if we use dynamic programming we can improve it):

f(0) = 0
f(1) = 1
f(n) = f(n-1) + f(n-2)

Recursion is not always visible from the problem definition.

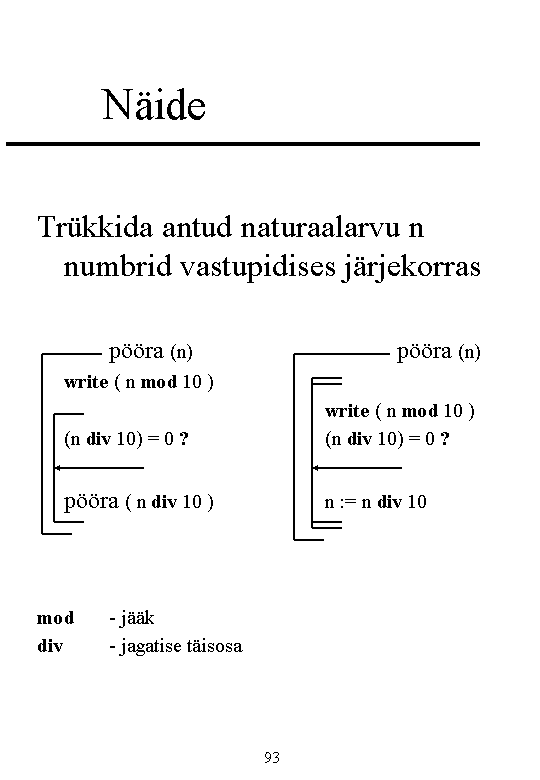
Example. Tower of Hanoi

Exponential time complexity

Reasoning:

Base case: If there are no disks, the problem is solved.

Step: If we can move  k-1 disks from peg a to peg b then to move k disks from peg x to peg z we need to:

1. Move k-1 disks from peg x to peg y (we can do it by assumption);
2. Move the largest disk (k) from peg x to peg z ("bottom");
3. Move those k-1 disks from peg y to peg z (we still can do it).

It is important that initial state (or any other state) of this game is allowable.

Code

  public static void hanoi (int n, int x, int y, int z) {
      if (n > 0) {
         hanoi (n-1, x, z, y);
         System.out.print (String.valueOf(x) + ">" + String.valueOf(z) + " ");
	 hanoi (n-1, y, x, z);
      }
  }

    

Removing the recursion

General one parameter function p(n):

Special case: tail recursion

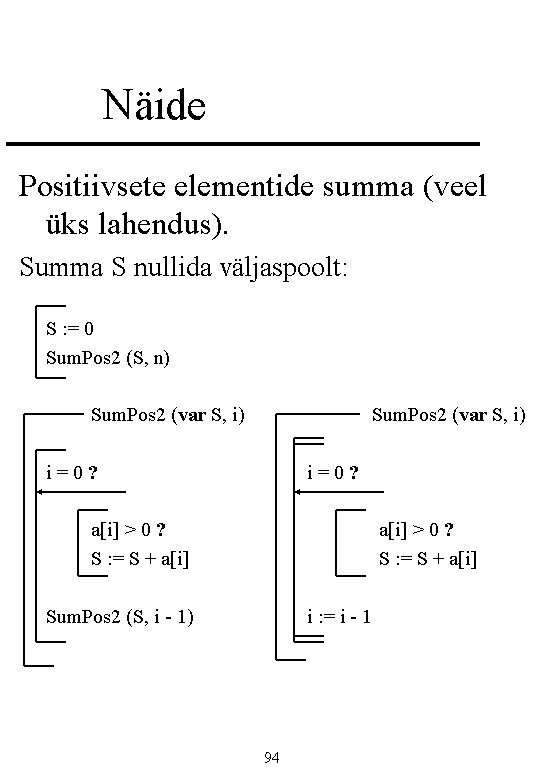
Tail call

Exhaustive search

There are problems which can only be solved by "trying" all the possible answers (assume we can check the answer).
Finite n-element set has 2ⁿ different subsets and if we need to check these all, it takes exponential time. We still can improve exhaustive search ("brute force" search) by narrowing the search space.

Two main cases:

• Find the first solution
  
• Find all solutions (there must be finite number of these)
  

From graph traversal: DFS and BFS illustrate those cases.

Backtracking - happens, if there are no more choices left in current situation. Then we step back and choose the new alternative on previous level.

Example. 8 queens - find all solutions.
Place 8 queens on 8x8 board without attacking each other.








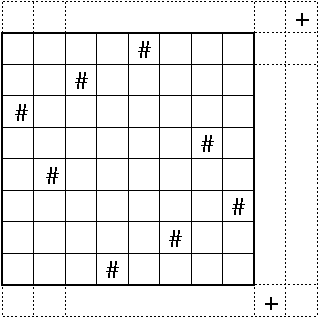
Code for n queens problem

Example. Sudoku

Example. Knight tour (DFS)

Knapsack problem

We have n>0 items with strictly positive weights and strictly positive costs (values). We have to choose such a set of items that does not exceed the weight limit b>0 and is maximally valueable (sum of costs of items is maximal).

Start similar to 8 queens: choose an item, if it fits (sum of weights does not exceed the limit) then take it and continue to next item, if it does not, leave it and continue to next item.
If you have decided about all items, remember the sum of weights and the sum of values for this set (also remember the set, of course). If the set is better than the set known before, forget the previous set.
To get to the next set move up (see the figures) using left branches of the decision tree, then move up using right branches and then backtrack (throw out one previously chosen item). Continue moving down after backtracking (without exceeding the limit) until you get the next set. If no more choices are left, finish and report the best set.

Overall strategy: cut the decision tree as high (near to the root) as possible.

Code for knapsack problem

---

J. Pöial