Binary
Search Tree, Binary Heap
Binary
tree, perfect binary tree, complete binary tree, traversal
of a binary tree. Binary search tree. Searching, adding, deleting
nodes from BST. Balancing.
Binary heap. Up-heap and down-heap bubbling. Heapsort method.
Binary Tree
A binary tree is
a tree data structure in which each node has at most two children, which are referred to as
the left child and the right child.
Corollary: if the node has exactly one child, it is important to
know which one (left or right).
T is a binary tree, if either:
- T is empty
or
- T = (t0, Tl, Tr),
where t0 is the root of tree T, Tl
is a binary tree (left subtree) and Tr is a binary
tree (right subtree).
Perfect (complete) binary
tree is a binary tree in which all interior
nodes have two children and all leaves have the same depth
or same level;
Complete (almost
complete) binary tree is a
perfect tree whose rightmost leaves (perhaps all) have been
removed.
Traversal of a Binary Tree
Pre-order:
If T is not empty:
- Process the root node
- Apply pre-order to the left subtree
- Apply pre-order to the right subtree.
Post-order (end-order):
If T is not empty:
- Apply post-order to the left subtree
- Apply post-order to the right subtree
- Process the root node.
In-order:
If T is not empty:
- Apply in-order to the left subtree
- Process the root node
- Apply in order to the right subtree.
Binary Search Tree
Let each node t contain a
comparable key t.x.
Let T.x be a key of the root node of a non-empty binary
tree T.
Binary search tree is a
binary tree T where either:
T is empty
or
- for each node tl from the left subtree Tl
: tl.x <= T.x
- for each node tr from the right subtree Tr
: tr.x >= T.x
- Tl and Tr are binary search
trees.
Building a binary search tree = sorting (traverse the tree
in in-order)
Balanced binary tree
keeps Tl and Tr more or less of equal
height (e.g. AVL-tree allows height difference 1 level).
Operations
Search: Average time complexity O(h), where h is the
height of the tree
search (T, key):
1. if T is empty return failure
2. if key==T.x return the root of T
3. if key < T.x search (Tl , key)
4. if key > T.x search (Tr , key)
Add: O(h)
add (T, R):
1. if R.x < T.x
a. if Tl is empty, add R as
the left subtree of T
b. if Tl is not empty add (Tl , R)
2. if R.x >= T.x
a. if Tr is empty, add R as
the right subtree of T
b. if Tr is not empty add (Tr , R)
Delete: O(h)
delete (T, key):
1. if T is empty do nothing
2. if key < T.x delete (Tl , key)
3. if key > T.x delete (Tr , key)
4. if key==T.x
a. if Tl is empty replace T
by Tr (root of T is deleted)
b. if Tr is
empty replace T by Tl (root of T is deleted)
c. if both subtrees are non-empty
R := removeSuccessor
(Tr )
store R in the root node of T
removeSuccessor (TR):
1. if TRl is empty
a. R:= info inside TR
b.TR is replaced by TRr (root of TR is deleted)
c. R is returned as the result
2. if TRl is
non-empty removeSuccessor (TRl
)
These operations are O(h), but they do not keep
the tree in balance.
Heap
Heap property: for any node t its key t.x is not
greater than the key of its parent (non-increasing chains of
keys from the root to each leaf).
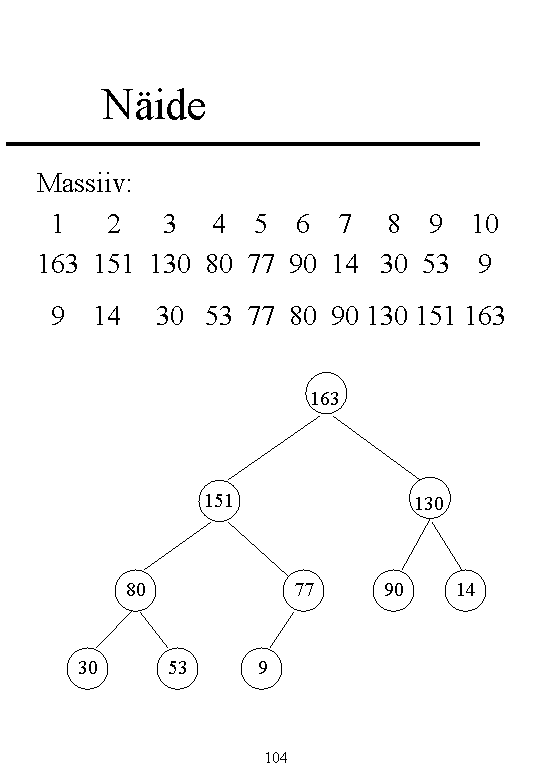
Binary heap is a
(almost) complete binary tree with the heap property. The
largest key is in the root node.
Inverse heap: replace "not greater" by "not smaller"
(non-decreasing chains, smallest key in the root).
Implementing a binary heap as an array:
1. Index of the root node is 1
2. If the index of the node is k, then index of the left subtree
root is 2k and index of the right subtree root is 2k+1
3. If the index calculated is bigger than the actual number of
elements than there is no node existing.
import java.util.*;
public class Heap {
/** Heap elements reside in an array. */
private int [] array;
Heap() {
this (20);
}
Heap (int size) {
array = new int [size+1];
array [0] = size;
if (size>0)
for
(int i=1; i<=size; i++)
array [i] = 0;
}
public int size() {
return array [0];
}
public void setSize (int size) {
array [0] = size;
}
public int set (int index, int element) {
int tmp = array [index];
array [index] = element;
return tmp;
}
public int get (int index) {
return array [index];
}
@Override
public String toString() {
StringBuffer sb = new
StringBuffer();
if (size() > 0)
for
(int i=1; i<=size(); i++)
sb.append (String.valueOf (array [i]) + " ");
sb.append
(System.getProperty ("line.separator"));
return sb.toString();
}
/** Left subtree index. */
public static int left (int rootindex) {
return 2*rootindex;
}
/** Right subtree index. */
public static int right (int rootindex) {
return 2*rootindex + 1;
}
/** Parent index. */
public static int parent (int index) {
return index / 2;
}
public boolean inside (int index) {
return (index >= 1)
&& (index <= size());
}
/** Fix the heap by moving big key up. */
public void moveUp (int i) {
int j = parent (i);
if (inside (j)) {
if (get
(i) > get (j)) {
int tmp = get (i);
set (i, get (j));
set (j, tmp);
moveUp (j);
}
}
}
/** Fix the heap by moving small key down.
*/
public void moveDown (int i) {
int j = left (i);
if (inside (j)) {
int k =
right (i);
if
(inside (k))
if (get (k) > get (j))
j = k; // j is bigger
if (get
(i) < get (j)) {
int tmp = get (i);
set (i, get (j));
set (j, tmp);
moveDown (j);
}
}
}
/** Remove the maximum element. */
public int takeMax() {
if (size() <= 0)
throw
new ArrayIndexOutOfBoundsException ("heap empty");
int result = get (1);
set (1, get (size()));
setSize (size() - 1);
moveDown (1);
return result;
}
public void addToHeap (int element) {
if (size() <
array.length - 1) {
setSize
(size() + 1);
set
(size(), element);
moveUp
(size());
}
}
public void makeHeap (int i) {
if (i <= size()) {
makeHeap (left (i));
makeHeap (right (i));
moveDown (i);
}
}
public static void heapSort (int n, int[]
sarray) {
if (n < 2) return;
Heap heap = new Heap (n);
for (int i=1; i<=n;
i++)
heap.set (i, sarray [i-1]);
heap.makeHeap (1);
for (int k=n-1; k>=0;
k--)
sarray
[k] = heap.takeMax();
}
public static void main (String[] params) {
int [] numbers = new int
[30];
Random generator = new
Random (new Date().getTime());
for (int i=0; i<30;
i++)
numbers
[i] = generator.nextInt (9999);
System.out.println
("Before:");
for (int i=0; i<30;
i++)
System.out.print (String.valueOf (numbers [i]) + " ");
System.out.println();
heapSort (30, numbers);
System.out.println
("After:");
for (int i=0; i<30;
i++)
System.out.print (String.valueOf (numbers [i]) + " ");
System.out.println();
}
}



 Code
Code
Jaanus Pöial