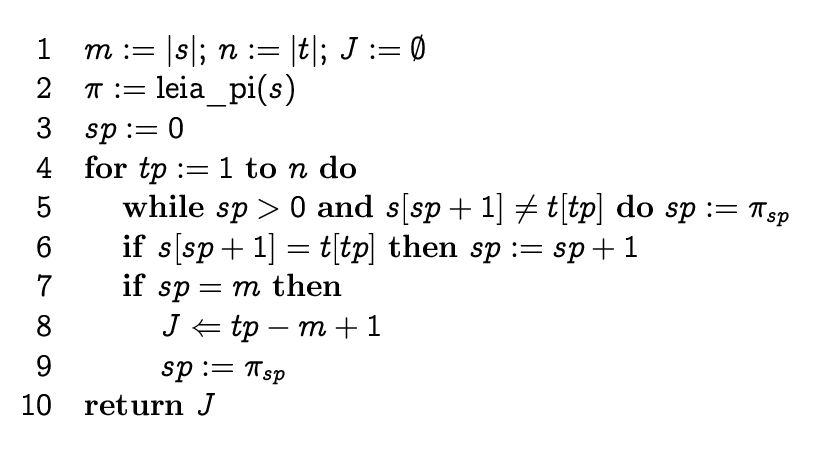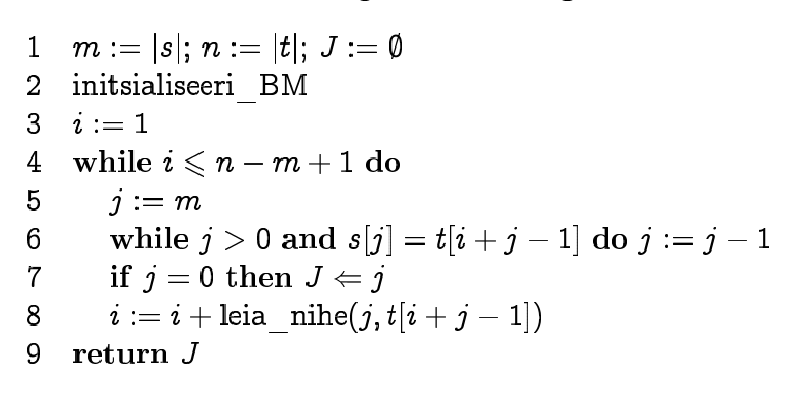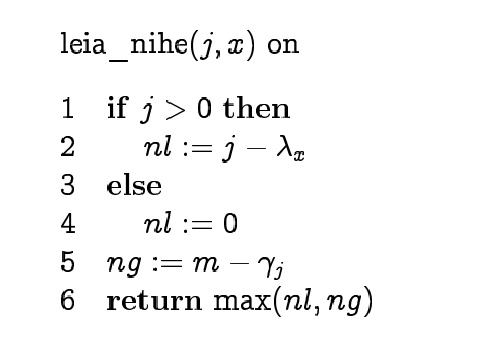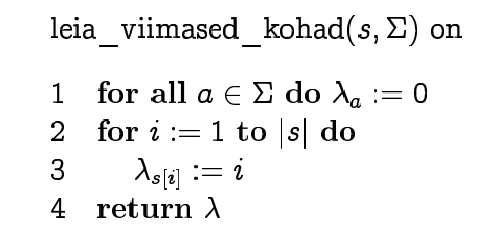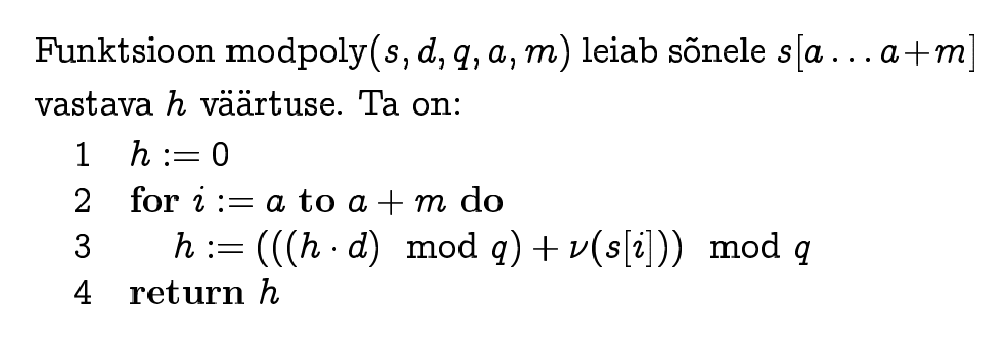String algorithms: exact matching (linear, Knuth-Morris-Pratt, Boyer-Moore, Rabin-Karp)

String, empty string, length of the string, substring in position i.
Classical text processing problem areas: pattern matching (exact, approximate, multi-pattern, n-dimensional, ...), editing distance, coding, compressing, search, indexing, ...
Exact matching: brute force, Knuth-Morris-Pratt algorithm. Prefix function (failure function), finite automaton. Complexity issues. Suffix function (looking glass heuristic) and last occurrence function (character jump heuristic), Boyer-Moore algorithm. Cyclic hash functions, Rabin-Karp algorithm.
Summary

Sõnetöötlus - alamsõne otsimine

Sõne = string: etteantud lõpliku tähestiku sümbolite jada: t[1] t[2]...t[n] ; tühisõne - tühi jada (pikkusega null).

Sõne pikkus - sümbolite arv sõnes, enamasti tegeleme selles vallas lõpliku pikkusega sõnedega (mis võivad küll olla väga pikad).

Alamsõne positsioonis i koosneb sõne t järjestikustest sümbolitest: t[i, ... , j] = t[i] ... t[j] ( 0 < i <= j <= |t| ), mittetühja alamsõne pikkus on j-i+1

Probleemid, millega tegeldakse:
  1. Etteantud mustri(te) otsimine tekstist: täpne vs. ligikaudne, üks vs. mitu mustrit, lineaarne vs. mitmemõõtmeline...
  2. Sõnedevaheline kaugus: kuidas ühest sõnest saada teist
  3. Ühise osasõne otsimine
  4. Pakkimine
  5. Infootsing, indekseerimine
  6. Seaduspärasuste avastamine
  7. ....

Täpne otsimine


Vt. ka animatsioone


Antud on:
  1. sõne t pikkusega n (n võib olla suur) - tekst
  2. sõne s pikkusega m (m <n) - muster, otsisõne
Leida: kõik positsioonid k, mille korral muster s esineb tekstis t positsioonis k

Naiivne algoritm selle ülesande lahendamiseks vaatab läbi kogu otsinguruumi, sobitades s kõikvõimalikesse positsioonidesse tekstis t, niisuguseid positsioone on n-m +1 tükki ja iga sobitus võtab halvimal juhul m võrdlust: seega on naiivse algoritmi keerukus O((n-m+1)m) ~ O(mn), m<n.




Knuth-Morris-Pratti algoritm

Naiivset algoritmi saab oluliselt parandada, analüüsides eelnevalt otsisõne struktuuri. Kui praegu "nihutatakse" mustrit igal sammul ühe positsiooni võrra, siis Knuth-Morris-Pratti algoritmis arvutatakse võimalikud nihked ette välja ning kantakse tabelisse, mida siis nihutamisel kasutatakse (tabelis sisalduvat nn. prefiksfunktsiooni võib tõlgendada ka lõpliku automaadi terminites).

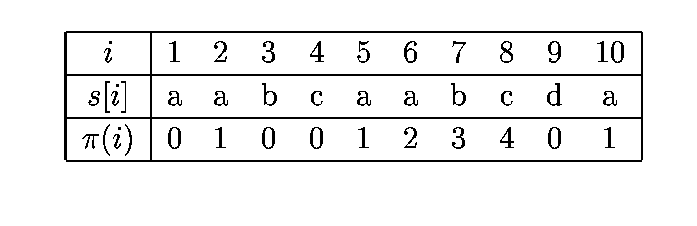
Prefiksfunktsiooni väärtus arvutatakse otsisõne s iga positsiooni i jaoks ning see on pikima sellise s prefiksi pikkus, mis on positsioonis i-1 lõppeva s alamsõne sufiksiks.













Automaadi terminites:

Olek
 sümbol -> olek
 sümbol ->olek
0 - algolek A -> 1
 not A -> 0
1 - A A -> 2
 not A -> 0
2 - AA B -> 3
 not B -> 1
3 - AAB C -> 4
 not C -> 0
4 - AABC A -> 5
 not A -> 0
5 - AABCA A -> 6
 not A -> 1
6 - AABCAA B -> 7
 not B -> 2
7 - AABCAAB C -> 8
 not C -> 3
8 - AABCAABC D -> 9
 not D -> 4
9 - AABCAABCD A -> 10
 not A -> 0
10 - AABCAABCDA, ACCEPT
 A -> 2
 not A -> 1

Saab näidata, et Knuth-Morris-Pratti algoritmi ajaline keerukus on O(m+n) koos lisamäluga O(m) prefiksfunktsiooni ettearvutamiseks.

Sama algoritm pseudokoodis




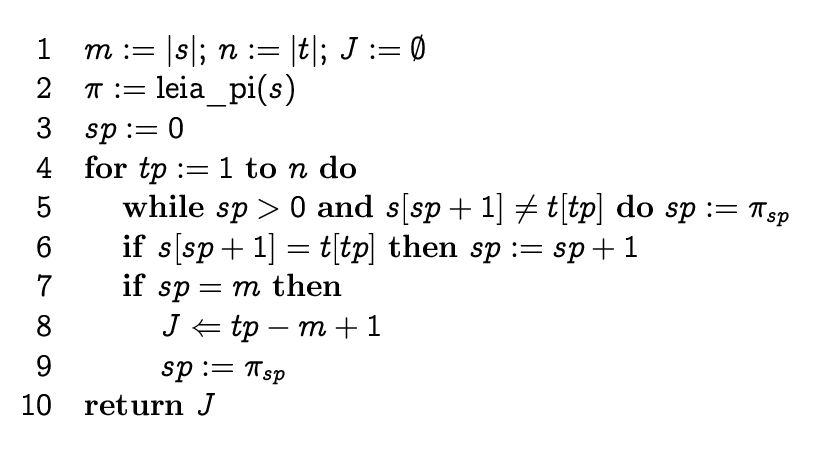
Kood

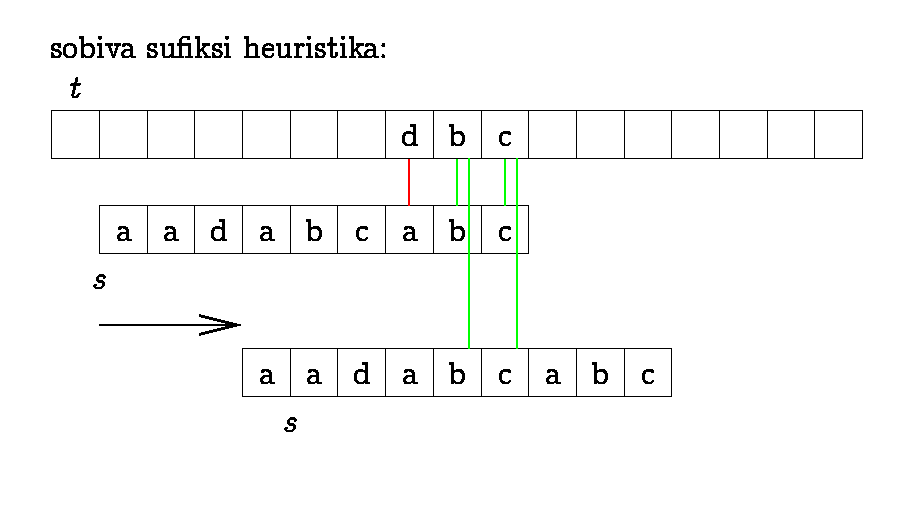
Boyer-Moore'i algoritm

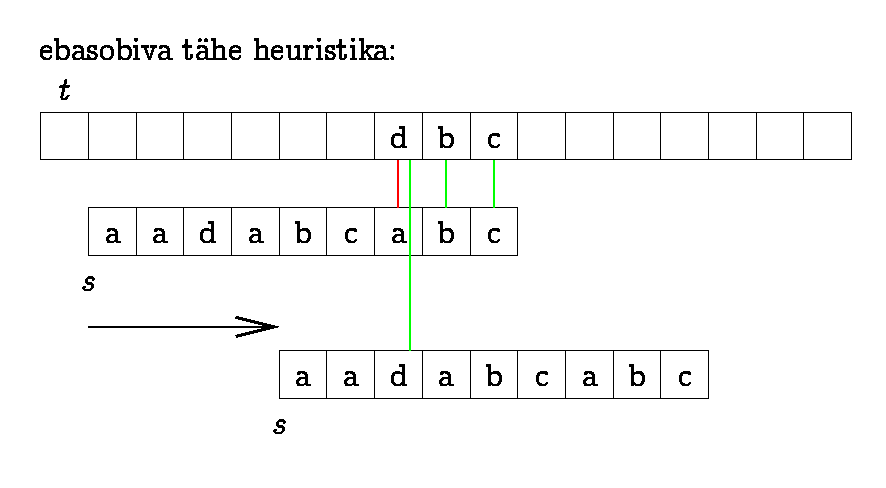
Ka Boyer-Moore'i algoritm pühendub "paremale hüppamisele" tekstis. Sobitamine toimub paremalt vasakule, prefiksfunktsiooni asemel arvutatakse sufiksfunktsioon ning lisaks veel sümboli nn. viimase esinemise funktsioon (iga sümboli viimase esinemise positsioon otsisõnes, mitteesinemisel null). Valitakse maksimaalne erinevate hüppevõimaluste vahel.
Praktikas saavutatakse oluliselt pikemad hüpped, ideaaljuhul taandub keerukus O(n/m)-ni, halvim keerukus on O(mn).
















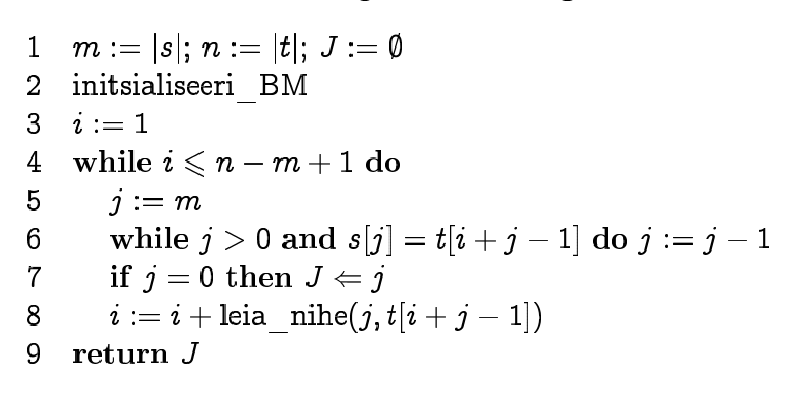
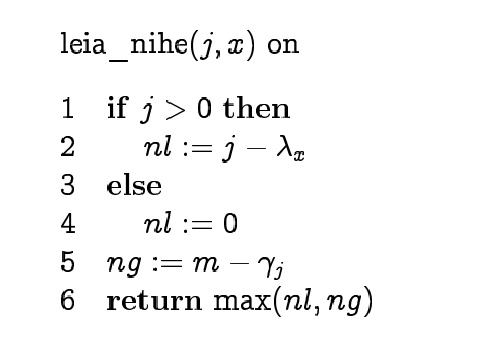
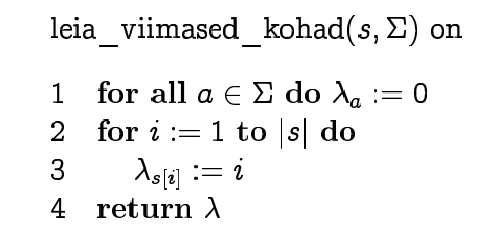
Sama algoritm pseudokoodis





Täiustatud variant:



Rabin-Karpi algoritm

Täpse otsimise ülesannet oleme siiani lahendanud jõumeetodi parandamise teel pikemate hüpete suunas. Teine lähenemine on parandada otsisõne ja vastava tekstilõigu võrdlemise kiirust (seni O(m)). Sõnede võrdlemise asemel võrdleme nende räsisid (potentsiaalse valehäire hinnaga). Räsifunktsiooni väärtust arvutame järgneva tekstilõigu jaoks kasutades eelmise lõigu räsi. Selline lähenemine töötab siis, kui m ei ole suur ja tähestiku võimsus ei ole suur. Olgu näiteks tähestik { 0, 1, 2, ..., 9 }. Siis iga sõnet selles tähestikus esindab täisarv, mille kümnendkujuks see sõne on. Selle arvu väljaarvutamise keerukus on O(m). Samas saab mustri nihutamist paremale arvutada kiiremini (lahutame räsi väärtusest suurima järgu, korrutame tähestiku võimsusega ning lisame uue vähima järgu). Valehäired tekivad sellest, et me arvutame mingis jäägiklassiringis (ei ole otstarbekas arvutada väga suurte täisarvudega). Seega tuleb räside kokkulangemisel alati kontrollida, kas ka sõned tegelikult kokku langesid.




Teistviisi:







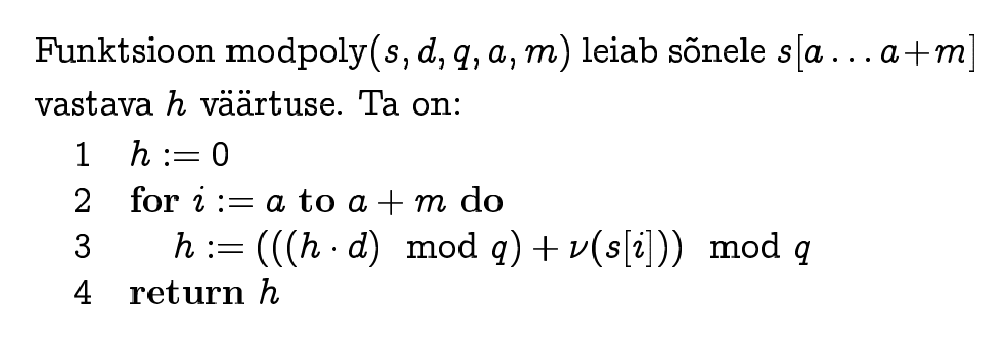
Jaanus Pöial