Binary Search Tree, Binary Heap, AVL-tree, B-tree, ...

Binary tree, traversal of a binary tree. Binary search tree. Searching, adding, deleting nodes from BST. Balancing.
Binary heap. Up-heap and down-heap bubbling. Heapsort method.
AVL-tree, rotation schemes (single rotation, double rotation).
Multi-way search tree, B-tree. Properties and updating operations: insert, overflow detection, split, remove, underflow detection, fusion (merge).
Binomial tree, red-black tree.

Kahendpuu, kuhi, AVL-puu, B-puu, jt.

Kahendpuu on puu, mille igal tipul on null kuni kaks alluvat, seejuures tehakse vahet vasakpoolse ja parempoolse alluva vahel.

T on kahendpuu, kui kas:
  1. T on tühi
või
  1. T = (t0, Tv, Tp), kus t0on puu T juur, Tv on kahendpuu (vasak alampuu) ja Tp on kahendpuu (parem alampuu).

Täielik kahendpuu sisaldab kõiki võimalikke tippe etteantud sügavusel (kõikidel vahetippudel on täpselt kaks alluvat);
kui eemaldada järjest parempoolseimaid lehti, on igal sammul tulemuseks kompaktne kahendpuu.

Kahendpuu läbimine

Eesjärjestuses (pre-order):
Kui T ei ole tühi, siis:
    1. töödelda juur
    2. läbida vasak alampuu eesjärjestuses
    3. läbida parem alampuu eesjärjestuses.
Taga- e. lõppjärjestuses (post-order, end-order):
Kui T ei ole tühi, siis:
    1. läbida vasak alampuu lõppjärjestuses
    2. läbida parem alampuu lõppjärjestuses
    3. töödelda juur.
Keskjärjestuses (in-order):
Kui T ei ole tühi, siis:
    1. läbida vasak alampuu keskjärjestuses
    2. töödelda juur
    3. läbida parem alampuu keskjärjestuses.







Kahendotsimise puu

Olgu kahendpuu iga tipuga t seotud võti t.x (võrreldavad väärtused).
T.x olgu mittetühja kahendpuu T juure võti.

Kahendotsimise puu on kahendpuu T, milles
  1. Kas T on tühi või

    1. iga tipu tv korral vasakust alampuust Tv kehtib tv.x <= T.x
    2. iga tipu tp korral paremast alampuust Tp kehtib tp.x >= T.x
    3. Tv ja Tp on kahendotsimise puud

Kahendotsimise puu moodustamine = järjestamine

Tasakaalustatud kahendpuu korral on Tv ja Tp enam-vähem võrdse suurusega (näit. kõrguste erinevus kuni 1).



Kuhi

Kuhjaomadus: puu ühegi tipu võti pole suurem kui tema ülemuse võti (mittekasvavad jadad juurest alla).

Kahendkuhi (edaspidi lihtsalt kuhi) on kuhjaomadusega kompaktne kahendpuu. Suurim võti on puu juurtipus.

Pöördkuhi: vahetame võrratusemärgi (ühegi tipu võti pole väiksem, kui tema ülemuse võti).

Kuhja kujutamine massiivina:

  1. Juure indeks on 1
  2. Kui tipu indeks on k, siis vasaku alampuu juure indeks on 2k ja parema alampuu juure indeks on 2k+1
  3. Kui arvutatud indeks on suurem elementide arvust kuhjas, siis vastav tipp puudub.













kood

Kahendotsimise puu operatsioonid, AVL-puu

Otsimine oli (eelpool vaadeldud) keerukusega O(log n), täpsemalt O(h), kus h on puu kõrgus



Lisamine on samuti O(h)



Eemaldamine on samuti O(h), aga nõuab vahel tipu järglase (keskjärjestuse mõttes) eemaldamist säilitades selle võtme eemaldatavas tipus


Järglase eemaldamiseks:


Kõik need operatsioonid sõltuvad puu kõrgusest h - seda tuleks hoida minimaalsena. Paraku ülaltoodud operatsioonid ei hoolitse puu kõrguse vähendamise eest.

AVL (Adelson-Velski, Landis) puu on kahendotsimise puu, mille korral:
  1. Vasak ja parem alampuu on AVL-puud ning nende kõrgused erinevad ülimalt ühe võrra.
  2. Tühi puu on AVL-puu.
Otsimine puud ei muuda ja on korraldatud samuti, nagu kahendotsimise puus.

Lisamine ja eemaldamine tuleb defineerida nii, et AVL-puu omadus säiliks, s.t. alampuude kõrguste vahe ei tohi olla suurem kui 1.

Pööre.Alampuude I ja III kõrgused enne pööret erinevad 2 võrra, omadus a≤b säilib.


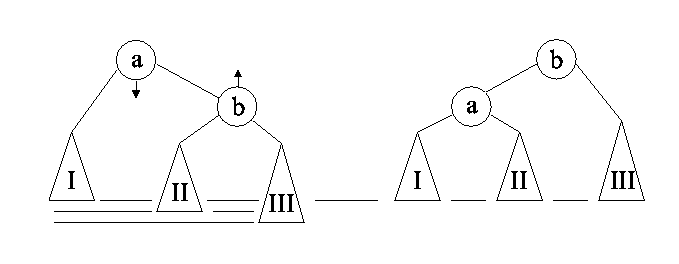Seda joonist võiks vaadata ka peegelpildis.


Topeltpööre. Alampuude I ja III kõrgused enne pööret erinevad 2 võrra, omadus a≤c≤b säilib.

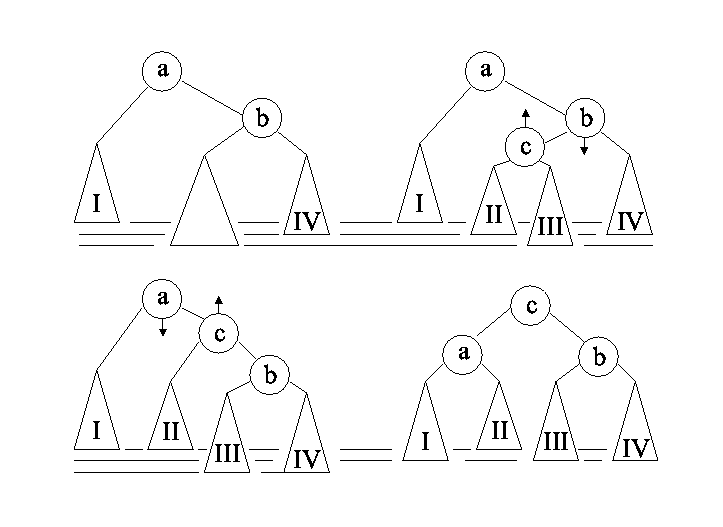Ka seda joonist võib vaadata peegelpildis.


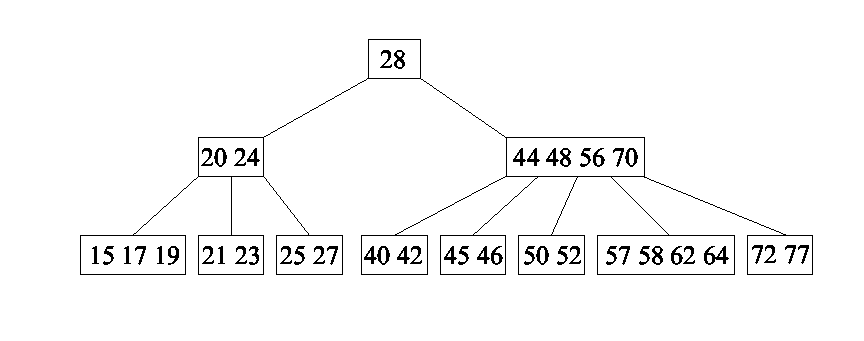
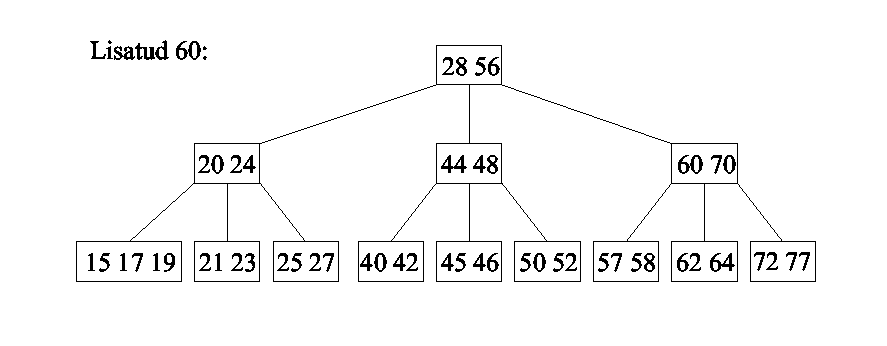
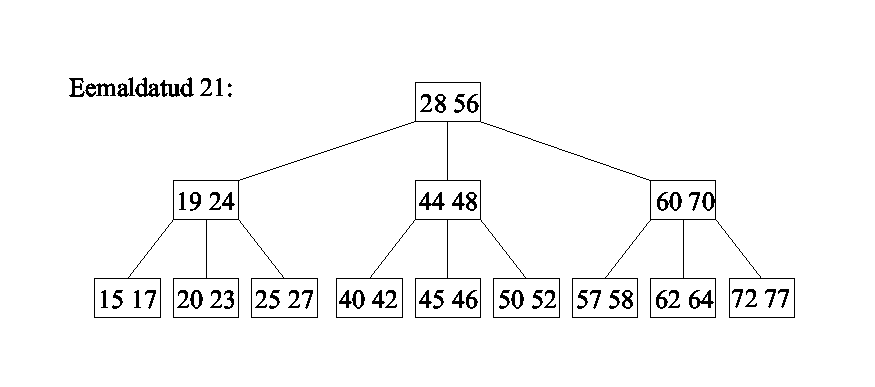
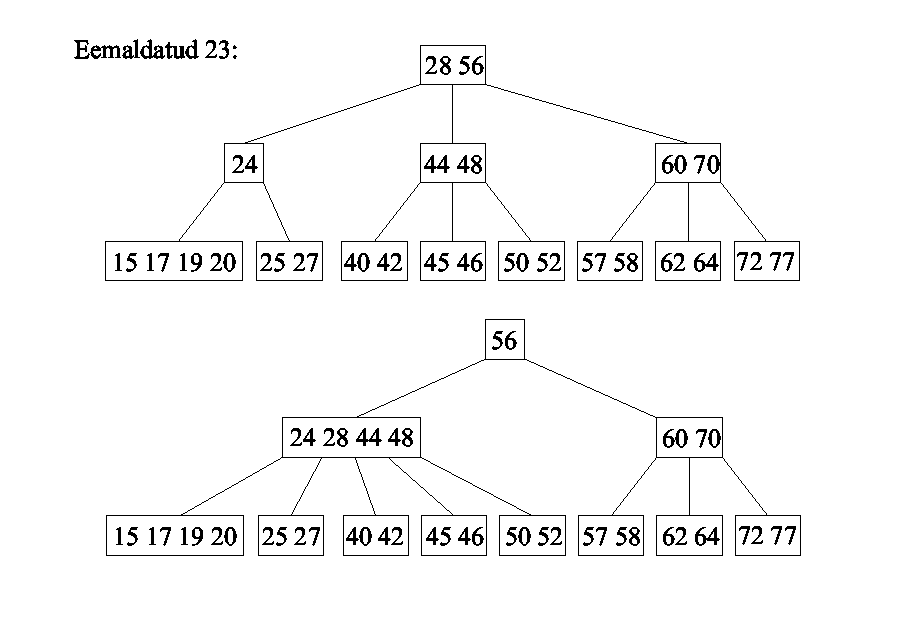
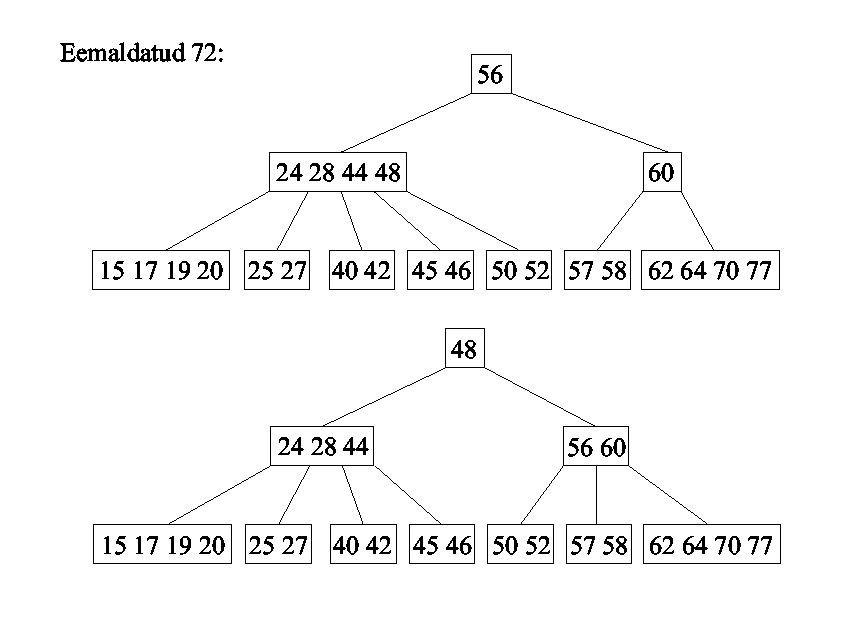
B-puu

Kahendotsimise puud võib üldistada m>2 juhtumile, lubades ühes puu tipus hoida kuni m-1 kirjet (m on konstant).


m-rajaline otsimispuu on kas:
  1. tühi või
  2. koosneb juurest, milles hoitakse järjestatuna j võtit (0<=j<m) ning j+1 alampuust, mis kõik peavad olema kas mittetühjad m-rajalised otsimispuud või (kõik) tühjad puud. Juure võtmete k1 <= k2 <= ... <= kj ja alampuude T0, T1, ... , Tj jaoks kehtivad järgmised kitsendused:
    1. kõik alampuus T0 esinevad võtmed k ei ületa juure esimest võtit k1: k <= k1
    2. kõigi võtmete k jaoks alampuust Ti (0<i<j) kehtib ki <= k <= ki+1
    3. kõik alampuus Tj esinevad võtmed k pole väiksemad kui juure viimane võti kj: k >= kj
m-järku B-puu (Bayer, McGreigh) on niisugune m-rajaline otsimispuu, milles
  1. kõik lehed on samal tasemel;
  2. lehed ei sisalda võtmeid (fiktiivsed, edaspidi jätame joonistel kujutamata);
  3. juurel on 2 kuni m alluvat;
  4. kõigil teistel vahetippudel on t=ceil[m/2] (t>=2) kuni m alluvat.
Seega on juures 1 kuni m-1 võtit, vahetippudes t-1 kuni m-1 võtit.


Tipp on täitunud, kui ta sisaldab m-1 võtit.

Kõrgus h <= log t ((n+1)/2)

Mahutavus n ~ O (2*(m/2)h)

3-järku B-puu = 2-3 puu (igal vahetipul 2 või 3 alluvat).

Otsimine: O(th)
Lõigu "poolitamise" asemel otsitakse õigest alamlõigust (igal sammul kuni m valikut, kuni h sammu).

Näide: 3-4-5 puu e. 5-järku B-puu

Lisame siia tipu 60, mis "ei mahu" oma õigele kohale madalaimal tasemel: sel juhul tuleb vastav tipp "poolitada" (rek. üles välja), s.t ületäitunud tipu asemele luuakse kaks "poolt" ning "keskmine" element viiakse sammu võrra üles.


Lisamise keerukus on O(th).

Kustutamine võib nõuda ülemuse ja kolleegide muutmist. Eemaldame tipu 21, mis toob kaasa "alatäitumise" (kompenseerimiseks 19 liigub üles ja 20 alla: nõutud omadused säilivad).

Eemaldades nüüd tipu 23 me kolleegilt juurde võtta ei saa, tuleb hakata tippe ühendama.Ka siin liigutakse alt üles.

Eemaldamisel võib olla vaja korraga nii kolleegilt juurdevõtmist kui ka ühendamist. Näiteks eemaldame nüüd tipu 72


Ka eemaldamise keerukus on siiski O(th).

Binomiaalpuu

On teisigi puustruktuure, mille kõrgus on O(log n).


Binomiaalpuu Bk defineeritakse rekurrentse seosega:
  1. B0 on ühetipuline puu;
  2. Bk (k>0) konstrueeritakse kahest binomiaalpuust Bk-1, pannes ühe teise juurtipu esimeseks alluvaks.
Binomiaalpuul Bk on järgmised omadused:
  1. puu kõrgus on k
  2. puu tippude arv on 2k
  3. suurima astmega tipp on juur, mille alampuudeks on Bk-1, Bk-2, ..., B0
Binomiaalpuu on "kreenis" vasakule, kuid see ebasümmeetia on hästi piiratud.

Nimetus tuleb sellest, et i-ndal tasemel on binoomkordaja (ki) tippu: näit B3 puhul: 1, 3, 3, 1

Värvitud kahendpuu ("red-black tree")

AVL-puudega sarnanev skeem, mis hoiab kahendpuu harud tasakaalus.

Lisame kahendotsimise puu tipule omaduse "värv" võimalike väärtustega punane ja must.

Värvitud kahendpuu on kahendotsimise puu, milles:
  1. Iga tipp võib olla kas punane või must
  2. Lehed (antud juhul fiktiivsed tühitipud) on mustad
  3. Punase tipu kõik vahetud alluvad on mustad
  4. Igal lihtteel juurest leheni on ühepalju musti tippe
Sellise puu kõrgus on maksimaalselt 2 log (n+1)
Otsimine, lisamine ja kustutamine töötavad O(log n) ajaga.
Sarnaselt AVL-puule, kasutatakse tasakaalustamiseks lokaalseid pöördeid, mis halvimal juhul levivad O(h) tipule.

Jaanus Pöial