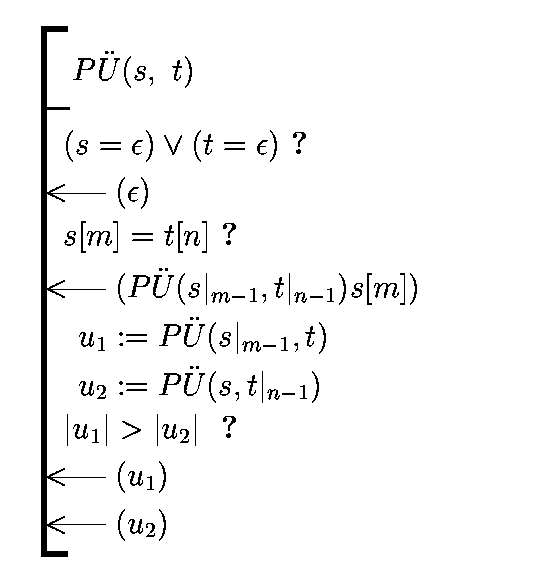Text Processing - Coding and Compressing

Greedy Strategies and Dynamic Programming

Encoding objectives: compression, error correcting, cryptology, ... Coding scheme: alphabet-based coding scheme (vs dictionary based or block encoding), single-valued (unique) coding scheme (vs lossy). Prefixcode, 0-1 prefixcode. Code tree for a prefix code. Compression using variable length code. Huffman code and Huffman algorithm (greedy). Encoding (compressing) and decoding (decompressing) using Huffman codes. Other methods for compression. Shannon-Fano method.

Dynamic programming. Fibonacci sequence. Longest common subsequence problem.

Sõnetöötlus - näited ahnest algoritmist ja dünaamilisest kavandamisest

Teksti kodeerimine ja pakkimine

Kodeerimine

Kodeerimisskeem on kujutus, mis seab lähtetekstile vastavusse kodeeritud teksti.

Tähestikupõhine kodeerimisskeem vaatleb lähteteksti sümbolite kaupa ning seab igale sümbolile vastavusse tema koodi.

Kui lähtetekst on koodi põhjal täpselt taastatav, siis nimetatakse seda üheseks kodeerimisskeemiks.

Üheses kodeerimisskeemis kadusid ei esine:
Viimast omadust saab tagada näiteks nn. prefikskoodide abil: ühegi sümboli kood ei ole mingi teise sümboli koodi prefiksis.

Vaatleme edasises juhtu, kus koodi väljendatakse kahendsüsteemis (0-1).
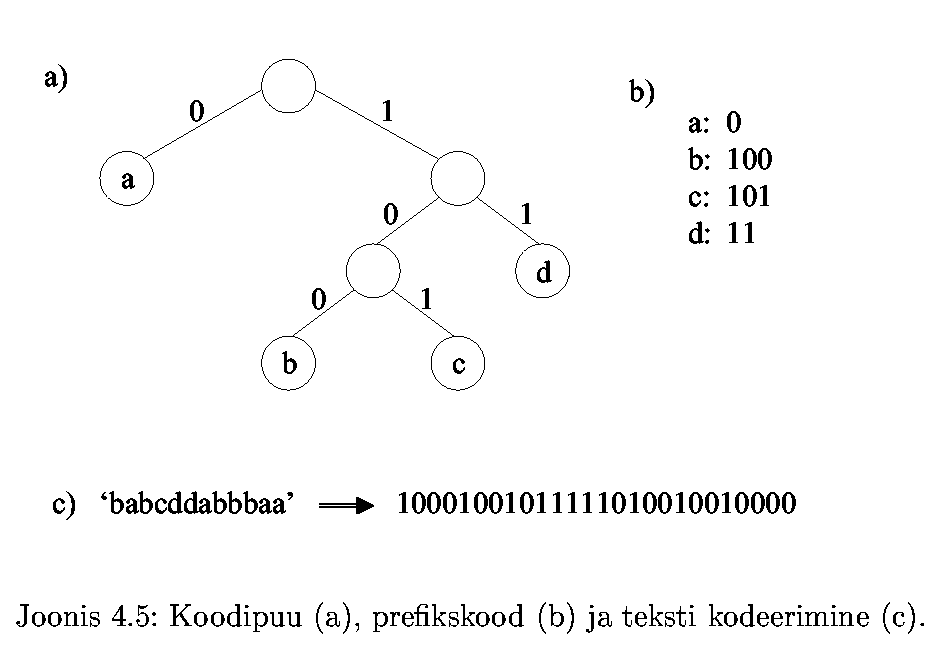
Siis saab kodeerimisskeemi kujutada kahendpuuna, mille lehtedeks on kodeeritavad sümbolid. Iga liikumine vasakusse alampuusse on kodeeritud nulliga, liikumine paremasse alampuusse ühega. Sümboli koodiks on bitijada, mis saadakse liikumisel selle kahendpuu juurest sümbolile vastava leheni.

Eelpool kirjeldatud puud nimetatakse antud sümbolite hulga koodipuuks. Tegemist on prefikskoodiga, sest:
"Tavaline" kodeering on täielik 8-tasemeline kahendpuu (igale sümbolile vastab bitijada pikkusega 8).

Pakkimine

Kokkuhoidu mälumahus saab saavutada näiteks kasutades muutuva pikkusega koode - sagedamini esinevatel sümbolitel on lühike kood, harvaesinevatel pikem. Vajame infot sümbolite esinemissageduse kohta.

 Prefikskoodi kasutamisel oleks vaja koodipuu koostada nii, et sagedamini esinevad sümbolid oleksid juurele lähemal, harvemesinevad kaugemal.




Huffmani puu antud teksti jaoks on niisugune koodipuu, mille abil kodeeritud teksti pikkus on minimaalne (kõikvõimalike koodipuude hulgas).

Huffmani puu moodustamine:
  1. Kodeeritava teksti eeltöötlus: teeme kindlaks tekstis esinevate sümbolite hulga ning iga sümboli esinemissageduse. Seda etappi ei pruugi teha, kui kasutame mingit standardset ja ettearvutatud sagedustega tähestikku (aga siis ei tule skeem optimaalne).
  2. Moodustame tulevase koodipuu lehed, säilitades neis sümbolit ning selle esinemissagedust. Iga lehte käsitleme alampuu juurena.
  3. Valime kaks alampuud, mille juurest võetud esinemissagedused on vähimad kõigi alampuude hulgas (kui kaht puud enam valida ei saa, siis on algoritm oma töö lõpetanud). Moodustame nende kohale uue vahetipu, millesse salvestame alluvate esinemissageduste summa ning paneme valitud alampuud selle vahetipu vasakus ja paremaks alluvaks.
  4. Jätkame sammuga 3 niikaua, kuni enam kaht puud valida ei saa.
See on nn. ahne (greedy) algoritm, milles optimaalne tulemus saavutatakse igal sammul selle hetke parimat jätku kasutades.



Pakkimiseks saab kasutada ka teisi meetodeid: näit sarnaste korduvate lõikude järjendi asendamine paariga <korduste arv, korduv lõik>, järjestikuste nullide/ühtede puhul piisab ainult kordajate jadast.

Shannon-Fano meetodil prefikskoodi moodustamine: sümbolihulkade poolitamine.

Ziv-Lempeli meetod on adaptiivne - kodeerimisskeem (sõnastikuna) luuakse dünaamiliselt lähtesõne ühekordse läbivaatuse käigus.

Pakkimine võib olla ka kadudega - heli-, video- ja pildifailides võib inimesele nagunii mittetajutavad nüansid jätta taastamata.
Sellel põhineb ka info "peitmine" - steganograafia .


Pikima ühise osasõne otsimine

Osasõne on saadud antud sõnest (võib-olla) migite sümbolite väljajätmise teel. Iga sõne osasõnedeks on tühisõne ja see sõne ise, kokku on variante halvimal juhul 2n, kus n on sõne pikkus (halvim juht realiseerub näiteks siis, kui kõik sümbolid on erinevad).

Olgu antud sõne s pikkusega m ja sõne t pikkusega n. Leida niisugune sõne u pikkusega k, et u oleks nii s kui ka t osasõneks ja k oleks maksimaalne kõigi võimaluste hulgast. Selle ülesande lahend ei pruugi olla ühene - ühepikkuseid pikimaid ühiseid osasõnesid võib olla mitu (aga pikkus k on üheselt määratud).

Paneme tähele järgmisi tõsiasju:
  1. Kui s ja t lõpud langevad kokku, siis on see ühine lõpp ka lahendi u lõpp ja me saame ülesande taandada selle lõpu võrra lühemate sõnede juhtumile. Kui see nii ei oleks, siis saaksime sõnet u pikendada, aga u on eelduse kohaselt pikim.
  2. Kui s ja t viimased sümbolid ei lange kokku, siis valime s ja t hulgast selle, kumba viimane sümbol ei lange kokku u viimase sümboliga, ning eemaldame selle sümboli (tegelikult võiks lõpust eemaldada sümboleid kuni jõutakse u viimase sümboli esinemiseni) ja taandame ülesande lühema sõne juhtumile (u jääb samaks).
Seega saaks lahendit leida järgmise (ebaefektiivse) rekursiivse algoritmiga:


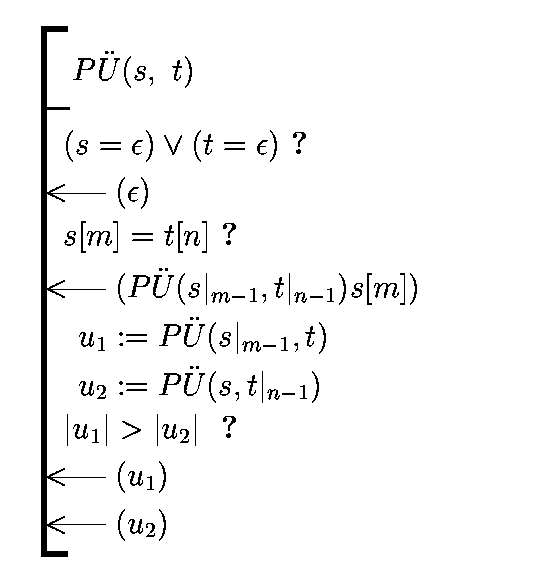See on väga ebaefektiivne korduvalt samade alamülesannete lahendamise tõttu. Otstarbekas oleks alamülesannete vastused meeles pidada ja neid kasutada ülesande lahendamiseks (vrd. Fibonacci arvude arvutamine). Niisugune lähenemine kattuvate alamülesannetega algoritmile kannab nimetust dünaamiline kavandamine.

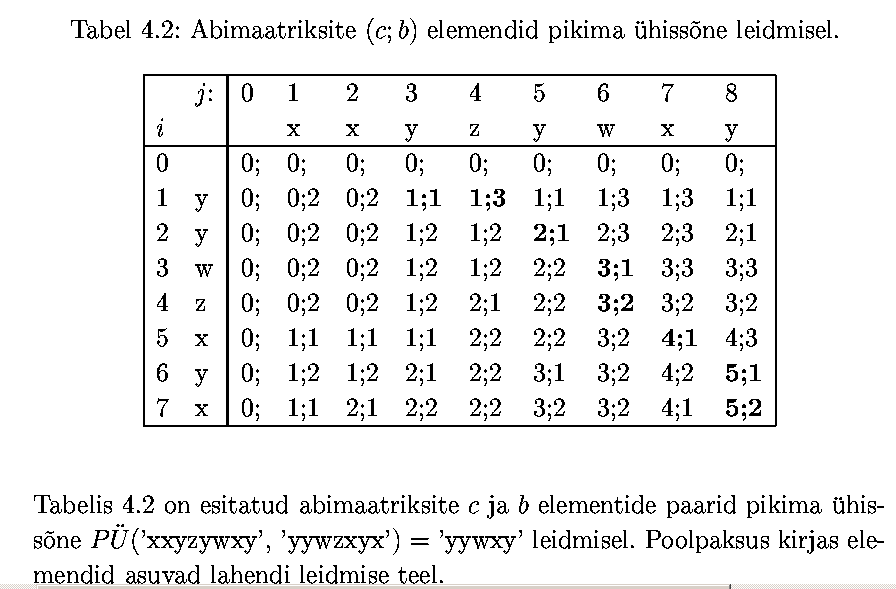
Antud ülesande jaoks koostame m x n abimaatriksi, mille element indeksitega i,j on s|i ja t|j pikima ühise osasõne pikkus.Rajatingimustena lisame maatriksile nullinda rea ja nullinda veeru, mille elementide väärtused on nullid. Arvutame selle tabeli ette välja: keerukus O(mn).




Vastuse saab tabelist välja lugeda: selle moodustavad need sümbolid s[i] (või t[j]), kus i, j > 0, mille korral c[i-1, j-1]+1 = c[i, j]


#!/usr/bin/env python3

import sys


def main():
    if len(sys.argv) > 2:
        s = sys.argv[1]
        t = sys.argv[2]
    else:
        s = "yywzxyx"
        t = "xxyzywxy"
    m = len(s)
    n = len(t)
    c = [[0]*(n+1) for row in range(m+1)]
    b = [[0]*(n+1) for row in range(m+1)]
    print("s =", s)
    print("t =", t)
    program(s, t, b, c)
    print(b)
    print(c)
    lcs = find_solution(s, t, b, m, n)
    print(lcs)


def program(s, t, b, c):
    for i in range(len(c)):
        c[i][0] = 0
    for j in range(len(c[0])):
        c[0][j] = 0
    for i in range(1, len(c)):
        for j in range(1, len(c[0])):
            if s[i-1] == t[j-1]:
                c[i][j] = c[i-1][j-1] + 1
                b[i][j] = 1
            elif c[i-1][j] > c[i][j-1]:
                c[i][j] = c[i-1][j]
                b[i][j] = 2
            else:
                c[i][j] = c[i][j-1]
                b[i][j] = 3


def find_solution(s, t, b, i, j):
    revlcs = ""
    while i > 0 and j > 0:
        if b[i][j] == 1:
            i = i - 1
            j = j - 1
            if s[i] != t[j]:
                raise ValueError("lahendi viga", i, j)
            revlcs += s[i]
        elif b[i][j] == 2:
            i = i - 1
        elif b[i][j] == 3:
            j = j - 1
        else:
            raise ValueError("tabeli viga", i, j)
    return revlcs[::-1]  # reverse



      .

    

    

    
Jaanus Pöial