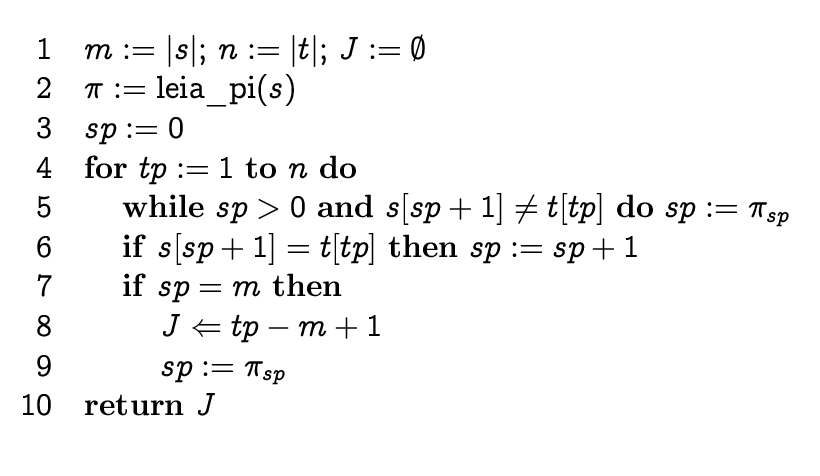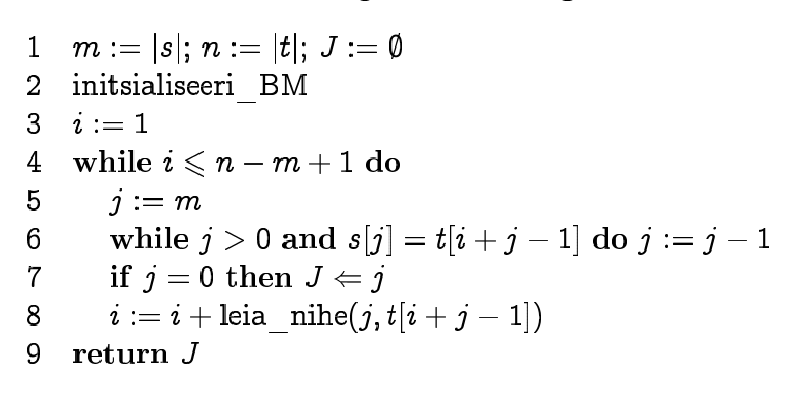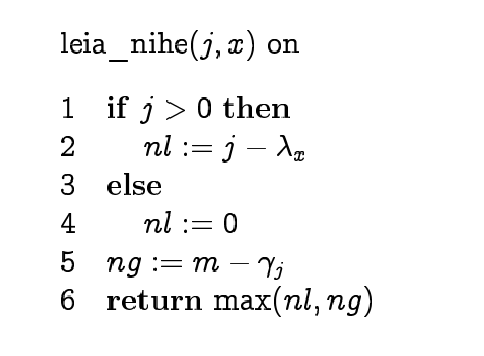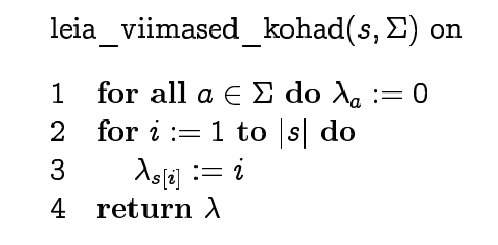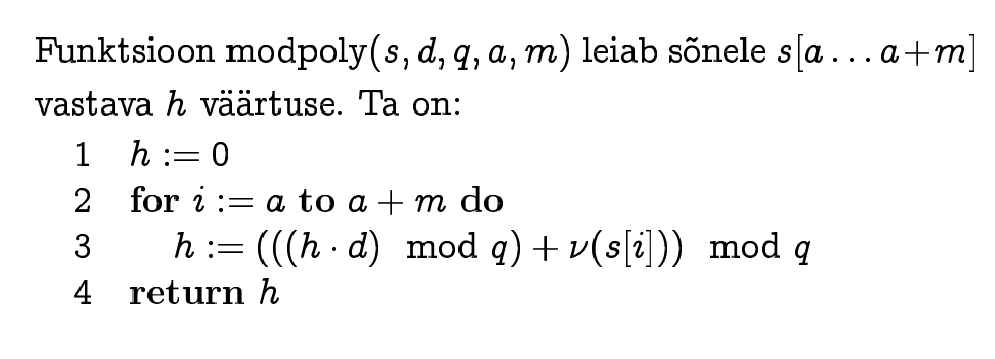String
Algorithms: Exact Matching (Linear, Knuth-Morris-Pratt,
Boyer-Moore, Rabin-Karp)
String,
empty string, length of the string, substring in position i.
Classical text processing problem areas: pattern matching (exact,
approximate, multi-pattern, n-dimensional, ...), editing distance,
coding, compressing, search, indexing, ...
Exact matching: brute force, Knuth-Morris-Pratt algorithm. Prefix
function (failure function), finite automaton. Complexity issues.
Suffix function (looking glass heuristic) and last occurrence
function (character jump heuristic), Boyer-Moore algorithm. Cyclic
hash functions, Rabin-Karp algorithm.
String Algorithms - Exact Matching
String: sequence of
characters from the finite alphabet: t[1] t[2]...t[n] ;
Empty string: empty sequence (sequence length is zero).
Length of a string: number of symbols in string; in our
case length is final (but maybe very long).
Substring of the string t in position i consists of
sequential symbols: t[i, ... , j] = t[i] ... t[j] ( 0
< i <= j <= |t| ), length of the substring is
j-i+1 (see also subsequence).
Classical text processing problem areas: pattern
matching (exact, approximate, multi-pattern, n-dimensional,
...), editing distance, coding, compressing, search, indexing,
...
Overview
of exact matching algorithms
Let us have:
- string t of length n (n is big) - text
- string s of length m (m <n) - pattern
Find: all positions k such that
pattern s is a substring of text t in position k
Naive algorithm (brute force):
/** Naive search.
* @param t text
* @param s search pattern
* @return list of positions (maybe empty)
*/
public static ArrayList<Integer>
posListNaive (String t, String s) {
if (t == null || t.length()
< 1) return null;
if (s == null || s.length()
< 1) return null;
if (s.length() > t.length())
return null;
int m = s.length();
int n = t.length();
ArrayList<Integer> p =
new ArrayList<Integer>();
for (int i=0; i < n - m + 1;
i++) {
int k = 0;
for (int j=0;
j < m; j++) {
if (s.charAt(j)==t.charAt(i+j))
k++;
else
break;
}
if (k == m)
p.add (i);
}
return p;
}
Time complexity of the brute force algorithm is O((n-m+1)*m) ~
O(n*m), m<n
Knuth-Morris-Pratt algorithm
We can shift the pattern by
more than one position, in case we analyze the pattern structure
beforehand.
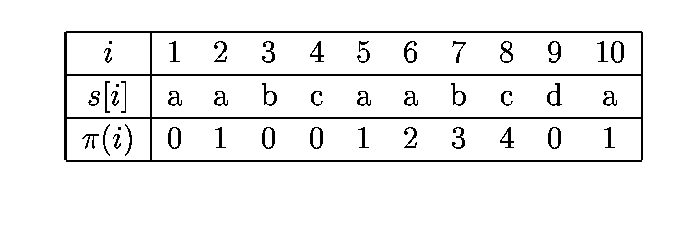
Prefix function (failure function) is defined for each
position i of the pattern s and it is equal to the length of the
longest prefix of s that is at the same time suffix of substring
of s of length i-1.
 /** Knuth-Morris-Pratt.
/** Knuth-Morris-Pratt.
* @param t text
* @param s pattern
* @param pi table of failure function
* @return list of positions
*/
public static ArrayList<Integer> posListJump
(String t, String s, int[] pi) {
if (t == null || t.length() <
1) return null;
if (s == null || s.length() <
1) return null;
if (s.length() > t.length())
return null;
if (pi == null || pi.length !=
s.length()) return null;
System.out.println ("Prefix
function for " + s + " is:");
for (int i=0; i < pi.length;
i++) {
System.out.print (pi[i]+" ");
}
System.out.println();
int m = s.length();
int n = t.length();
ArrayList<Integer> p = new
ArrayList<Integer>();
int i = 0;
for (int j=0; j < n; j++) {
while (i > 0
&& s.charAt(i) != t.charAt(j))
i = pi[i-1];
if (s.charAt(i)
== t.charAt(j)) i++;
if (i == m) {
p.add (j-m+1);
i = pi[i-1];
}
}
return p;
}
/** Calculate failure function for a given pattern.
* @param s pattern
* @return table of the function
*/
public static int[] prefTable (String s) {
if (s==null ||
s.length()==0)
return
null;
int m = s.length();
int[] res = new int [m];
res[0] = 0;
if (m < 2) return res;
// prefix function res
int k = 0; // length
for (int i=1; i < m;
i++) {
while (k
> 0 && s.charAt(k) != s.charAt(i))
k=res[k-1];
if
(s.charAt(k) == s.charAt(i))
k++;
res[i] =
k;
}
return res;
}
Prefix function can be interpreted by a finite automaton:
State
|
symbol -> state
|
symbol -> state
|
0 - initial state
|
A -> 1
|
not A -> 0
|
| 1 - A |
A -> 2
|
not A -> 0
|
| 2 - AA |
B -> 3
|
not B -> 1
|
| 3 - AAB |
C -> 4
|
not C -> 0
|
| 4 - AABC |
A -> 5
|
not A -> 0
|
| 5 - AABCA |
A -> 6
|
not A -> 1
|
| 6 - AABCAA |
B -> 7
|
not B -> 2
|
| 7 - AABCAAB |
C -> 8
|
not C -> 3
|
| 8 - AABCAABC |
D -> 9
|
not D -> 4
|
| 9 - AABCAABCD |
A -> 10
|
not A -> 0
|
10 - AABCAABCDA, ACCEPT
|
A -> 2
|
not A -> 1
|
Knuth-Morris-Pratt algorithm has time complexity O(m+n)
and space complexity O(m) to calculate the prefix function.
Pseudocode:
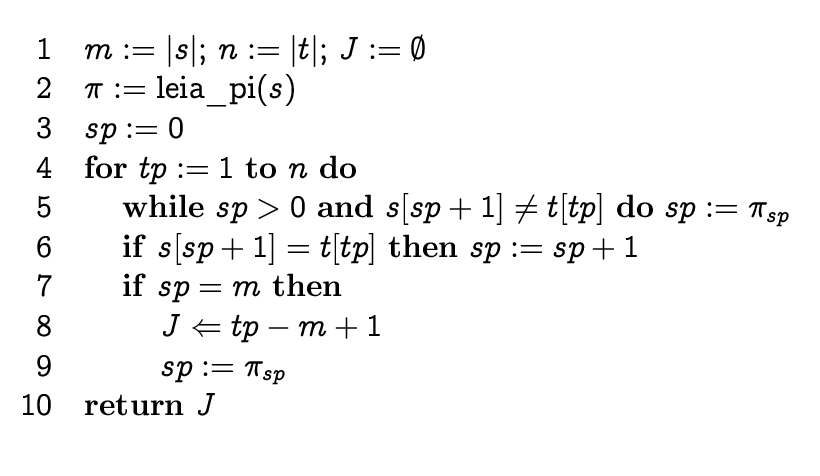
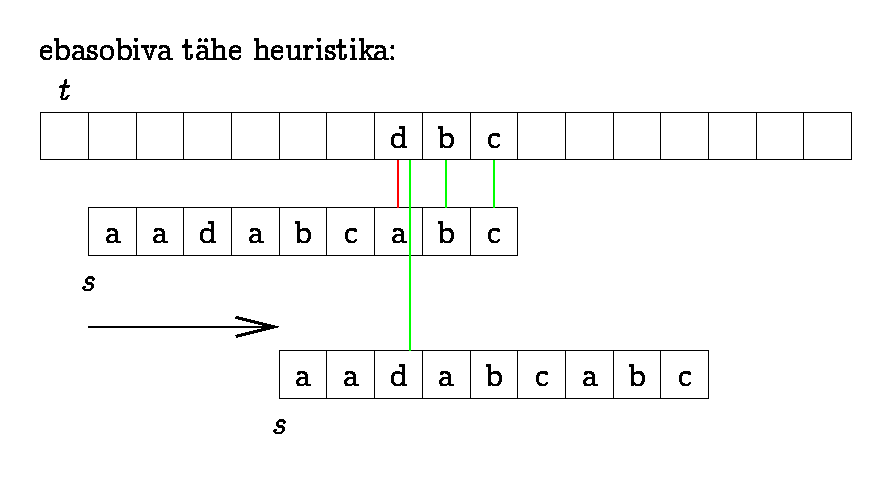
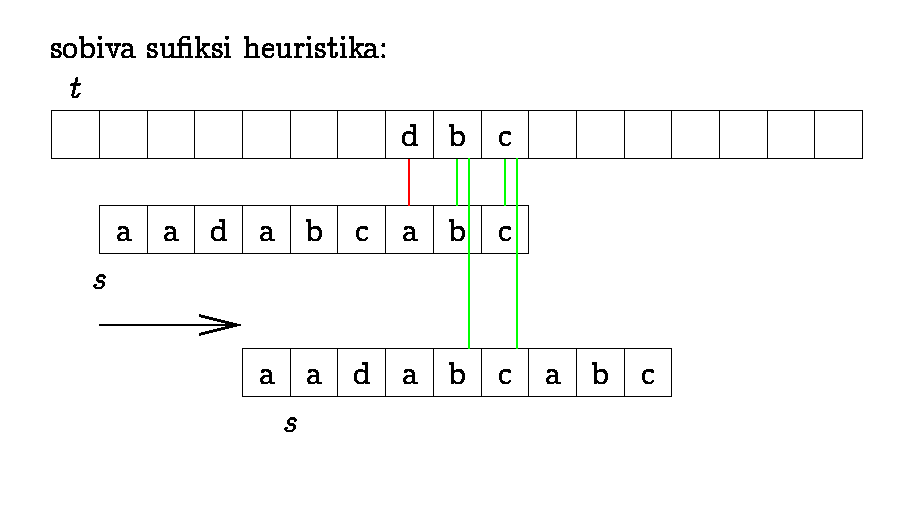
Boyer-Moore algorithm
We can improve KMP if we start
matching the pattern from right to left and use "character jump
function" together with suffix function.
We find which of the functions gives longer jump in each
situation. To make "character jumps" we find the position of the
last occurrence of each symbol in the pattern.
In practice, jumps are longer than in KMP.
Ideal case time complexity is O(n/m), worst case time complexity
is O(m*n).
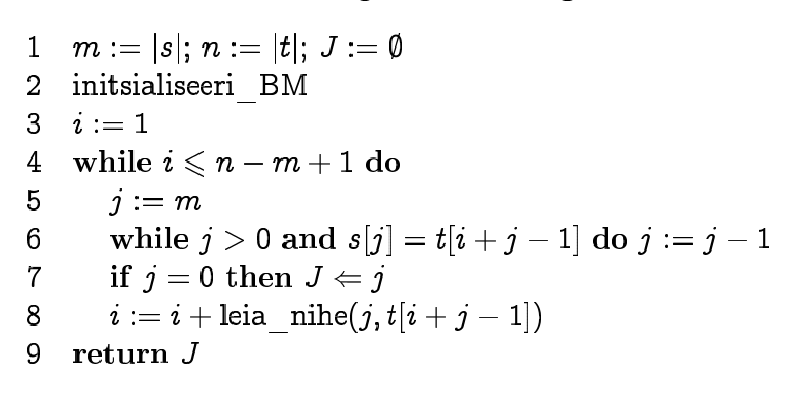
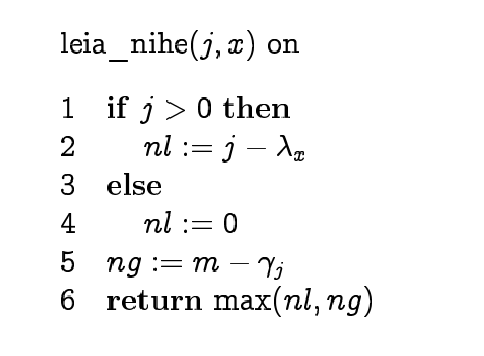

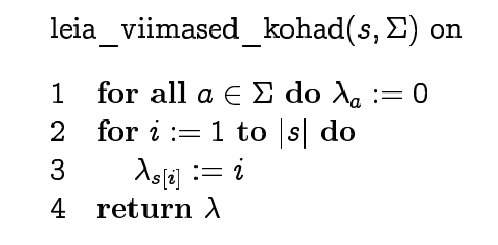
 Pseudocode
Pseudocode
 Improved version:
Improved version:

Rabin-Karp algorithm
Instead of string comparison
(complexity O(m) ) it is possible to calculate hashcodes of
strings and compare hashcodes only (complexity O(1) ).
If hashcodes are different, we can be sure that strings are
different.
If hashcodes are equal, we must compare strings explicitly, to
be sure that strings are equal (because collisions may happen).
NB! We assume that hash function is cyclic: if we shift the
"window" in text by one position, the new hashcode is calculated
from the old hashcode in constant time.


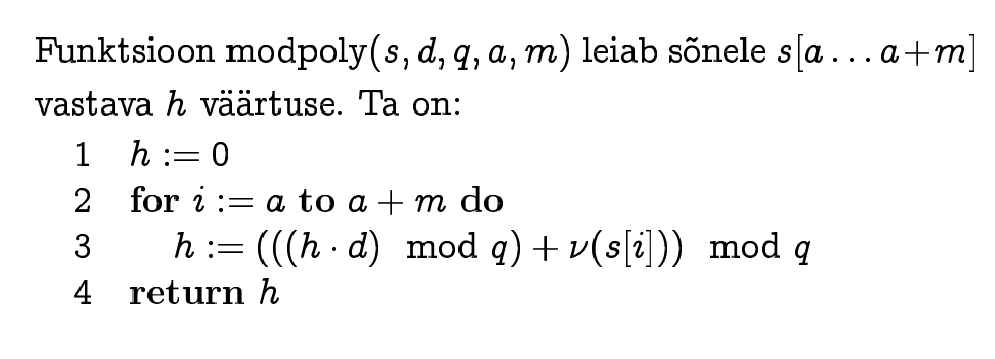
Jaanus Pöial