AVL-tree, B-tree, ...

AVL-tree, rotation schemes (single rotation, double rotation).
Multi-way search tree, B-tree. Properties and updating operations: insert, overflow detection, split, remove, underflow detection, fusion (merge).
Binomial tree, red-black tree.


AVL (Adelson-Velski, Landis) tree in a binary search tree where:
  1. Left and right subtrees are AVL trees and  difference of heights of subtrees is less or equal to one level.
  2. Empty tree is an AVL tree.

Searching does not change the tree and the usual binary tree search can be applied.
Adding and deleting must take care of balancing the tree to keep AVL property satisfied.


Single rotation. Read the in-order sequence of both trees:   I a II B III  to justify this operation. Difference 2 becomes difference 0.


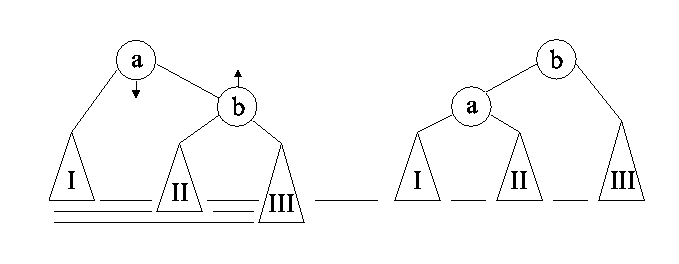The mirror of this scheme is also applicable: III b II a I .


Double rotation. I a II c III b IV.  Difference 2 becomes difference 1.

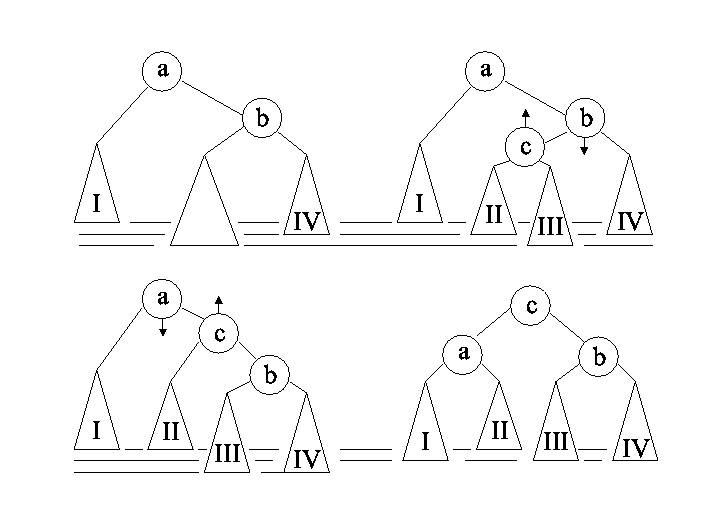Mirror: IV b III c II a I.


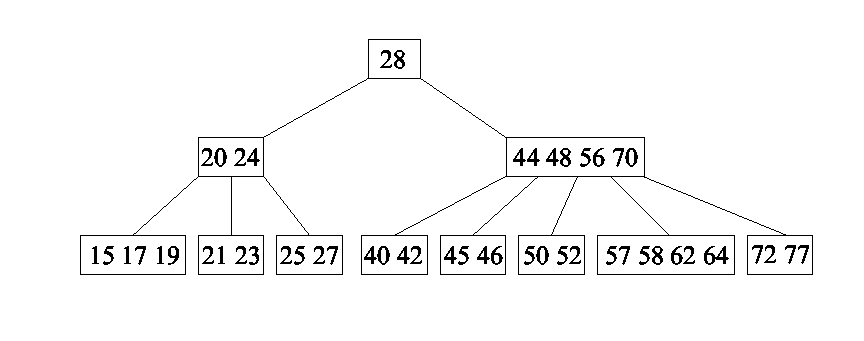
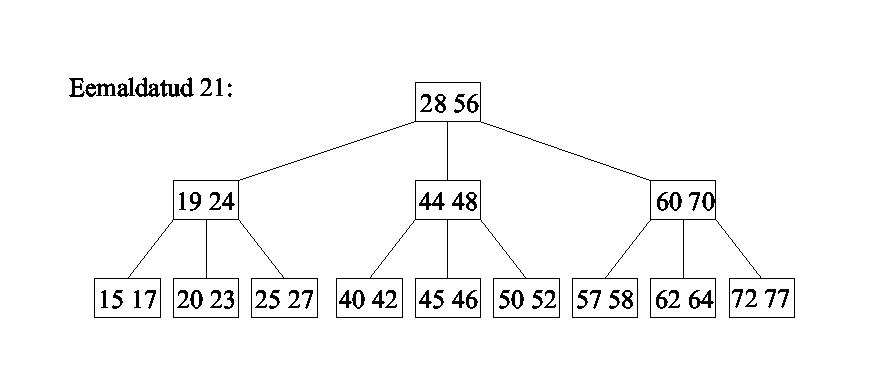
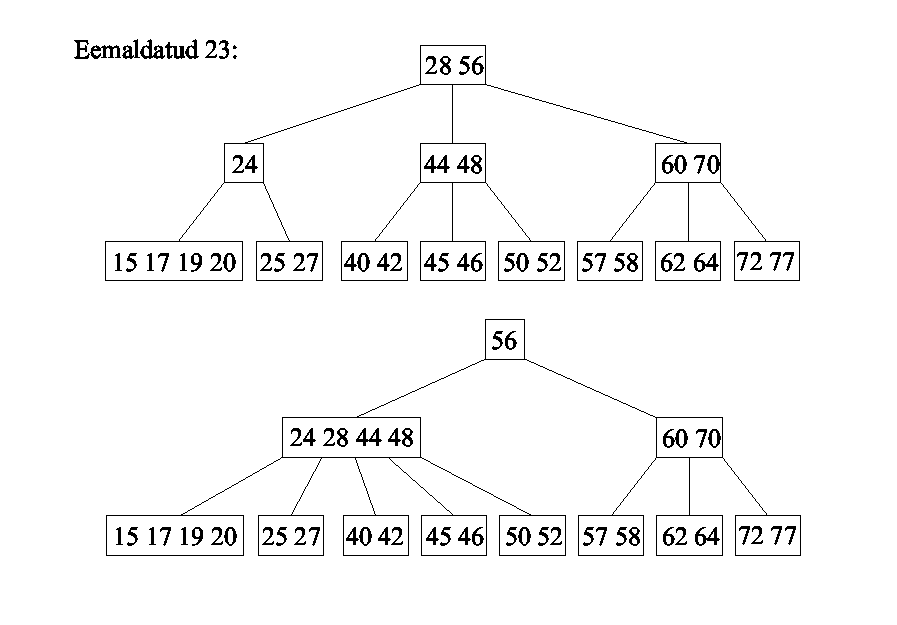
B-tree

Binary search tree has one key in each node and maximum two subtrees for each node.
Multi-way search tree has 1 .. m-1 keys in each node and maximum m subtrees for each node (m > 1 is a constant).

Multi-way search tree of order m (m-way search tree):
  1. is empty or
  2. has a root node with j  (0 < j < m ) keys and j+1 subtrees, that are ALL empty or ALL non-empty m-way search trees with the following key properties:
a)  for all keys k in subtree T0 : k <= k1
b)  for all keys k in subtree Ti (0<i<j) :  ki <= k <= ki+1
c)  for all keys k in subtree Tj : k >= kj
B-tree of order m (Bayer, McGreigh) is a m-way search tree where:
  1. all leaves are on the same level;
  2. leaves do not contain keys (empty);
  3. root node has 2 .. m subtrees;
  4. all other intermediate nodes have from  t=ceil[m/2]  (t>=2) to m subtrees.
Root node has from 1 to m-1 keys, intermediate nodes have from  t-1 to m-1 keys. Well balanced.

Node is full, if it contains m-1 keys.

Height of a tree: h <= log t ((n+1)/2)

Capacity (number of keys) n ~ O (2*(m/2)h)

B-tree of order 3 is also called 2-3 tree, B-tree of order 5 is called 3-4-5 tree etc.

Searching: O(th)

Example: 3-4-5 tree

Adding a new key 60 causes split:



  Adding: O(th).


  Deleting key 21 causes merge:



Deleting key 23 causes fusion:
  Deleting key 72 causes several changes


  Deleting: O(th).

Binomial tree

Height  O(log n).


Binomial tree Bk is defined by recursion:
  1. B0 is a one node tree;
  2. Bk (k>0) is constructed from two trees Bk-1, second tree is added to the first tree as the first child of the root.
Binomial tree Bk has the following properties:
  1. height of a tree is k
  2. number of nodes is 2k
  3. root node has the greatest number of subtrees:  Bk-1, Bk-2, ..., B0

Red-black tree

Similar to AVL-tree, but more relaxed and still balanced.

Each node of a binary search tree is red or black.

Red-black tree is a BST where:
  1. Each node is either red or black
  2. The root node is black
  3. All the leaves are black (empty nodes)
  4. All children of the red node are black
  5. Each path from the root node to any leaf node has the same number of black nodes in it
Maximal height: 2 log (n+1)
All operations take O(log n).

Slides

Jaanus Pöial