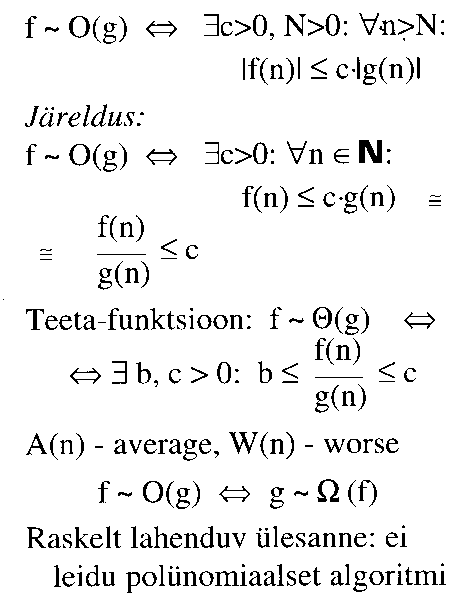Algoritmid
ca 825 m.a.j. , Abu Ja'far Mohammed ibn Mûsâ al-Khowârizmî -
reeglid aritmeetiliste operatsioonide sooritamiseks
Algoritm on täpne
(üheselt mõistetav) juhis antud ülesande lahendamiseks. Algoritm
koosneb lõplikust arvust sammudest,
millest igaüks on täidetav lõpliku aja jooksul lõplikke
ressursse kasutades. Algoritmi rakendatakse teatavale
lähteandmete komplektile (sisend)
ning ta annab teatava resultaadi (väljund).
Kui algoritm lõpetab töö (peatub) mistahes sisendi korral,
siis nim. seda kõikjal
määratud algoritmiks, vastasel juhul osaliseks algoritmiks.
Kui algoritmi mistahes sammu täitmise järel on üheselt
määratud, milline on järgmine samm, siis nim. algoritmi determineeritud algoritmiks.
Algoritmi iseloomustamiseks kasutatakse järgmisi mõisteid:
- Korrektsus
(algoritm lahendab "õiget" ülesannet, tulemus vastab
spetsifikatsioonile).
- Määratletus
(sammud on lõplikud ja üheselt määratud).
- Kirjelduse lõplikkus
(algoritm on kirjeldatav lõpliku arvu sammudega).
- Peatuvus. Töö
lõpetamine mistahes sisendi korral - kõikjal määratud
algoritm. Osaline e. "poollahenduv" algoritm kas annab
tulemuse või ei lõpeta tööd.
- Determinism
(samade algandmete korral vastus sama, lahenduskäik on
korratav) vs. mittedeterminism
(näit. "tõeline" juhuarvude generaator).
- Universaalsus
(lahendab probleemide klassi: sisend -> väljund ).
- Keerukus
(efektiivsus, kas lõpetamise aeg ja/või mälumaht on
praktilised).
Algoritmi formaalsed
(matemaatilised) esitused (samaväärsed):
- Turingi masin, 1936-37
- lambda-arvutus (Church), 1941
- Posti süsteemid, 1943
- Markovi algoritmid, 1951
- Chomsky 0-tüüpi grammatikad, 1959
- programmeerimiskeeled, Sammet, 1969
Algoritmiliselt mittelahenduvad ülesanded
Algorithms, well defined, total, partial,deterministic,
non-deterministic, correct (meet specification), halting.
Complexity of algorithms. Formal models of algorithms.
Algoritmi
keerukus
Keerukuse hindamine: ajaline ja mahuline keerukus
Ajaline keerukus
n - algandmete maht, f(n) > 0 - lahendamisaeg
- Asümptootilised hinnangud, "suure O", "väikese o",
"suure oomega", "väikese oomega" ja teeta-tähistused:
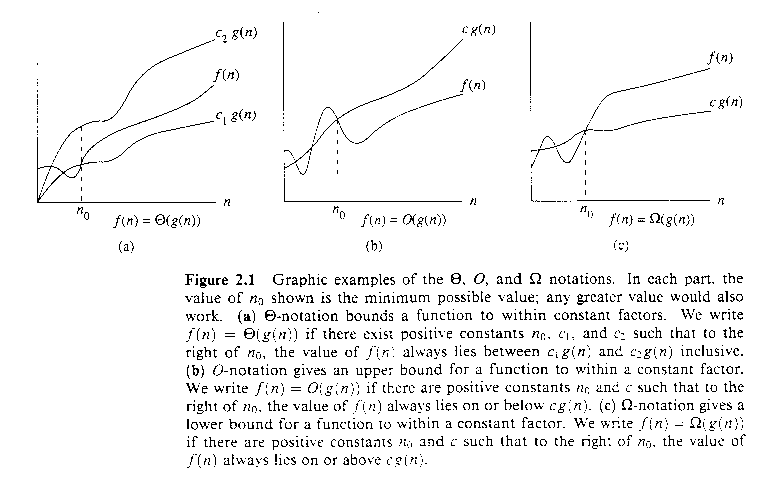
"f kasvab mitte kiiremini kui g" ( f big-Oh
g
)
- leiduvad konstant c>0 ja koht N nii, et iga n>N
korral
|f(n)| < c|g(n)|
f ja g suhe on ülalt tõkestatud.
"f kasvab aeglasemalt kui g" ( f little-oh g ) -
mistahes konstandi c>0 jaoks leidub koht N nii, et iga
n>N korral
|f(n)| < c|g(n)|
f ja g suhe pole alt tõkestatud.
"f kasvab niisama kiiresti kui g" ( f big-Theta g
) - leiduvad konstandid b, c>0 ja koht N nii, et
iga n>N korral
b|g(n)| < |f(n)| < c|g(n)|
f ja g suhe on nii ülalt kui ka alt tõkestatud.
"f kasvab mitte aeglasemalt kui g" ( f big-Omega
g ) - "g kasvab mitte kiiremini kui f"
f ja g suhe on alt tõkestatud.
"f kasvab kiiremini kui g" ( f little-omega g ) - "g
kasvab aeglasemalt kui f"
f ja g suhe pole ülalt tõkestatud.
iga konstandi a>0 korral f(n) ~ O(af(n))
kui f(n)<g(n) ja g(n) ~ O(h(n)), siis f(n) ~
O(h(n))
kui f(n) ~ O(g(n)) ja g(n) ~ O(h(n)), siis f(n) ~
O(h(n)) Tõestuse näide
f(n)+g(n) ~ O(max{f(n), g(n)})
kui g(n) ~ O(h(n)) , siis f(n)+g(n) ~ O(f(n)+h(n))
kui g(n) ~ O(h(n)), siis f(n)g(n) ~ O(f(n)h(n))
kui f(n)=p0+p1n+...+pknk
on k astme polünoom, siis f(n) ~ O(nk)
iga naturaalarvu k korral nk ~ o(2n)
iga naturaalarvu k korral log nk = k log n ~
O(log n)
Logaritmidega manipuleerimisel: logbn = logan
/ logab ning alogan
= n
- Keskmine ajaline keerukus A(n) ja ajaline keerukus
halvimal juhul W(n)
- Levinumad keerukusklassid: O(1), O(log
n),O(sqrt(n)),O(n), O(nlogn), O(n2), O(n2logn),
O(n3), ... , O(nk), O(2n),
O(n!), O(nn), O( 2^(2^(2^(...)))) n korda, kus ^
tähistab astendamist, ...
A(m,n)=A(m-1, A(m,n-1)), kui m>0 ja n>0,
A(0,n)=n+1,
A(m,0)=A(m-1,1), kui m>0
- "Mõistlik" piir on O(nk) ja O(2n)
vahel.
- Polünomiaalne keerukus, raskelt lahenduvad ülesanded
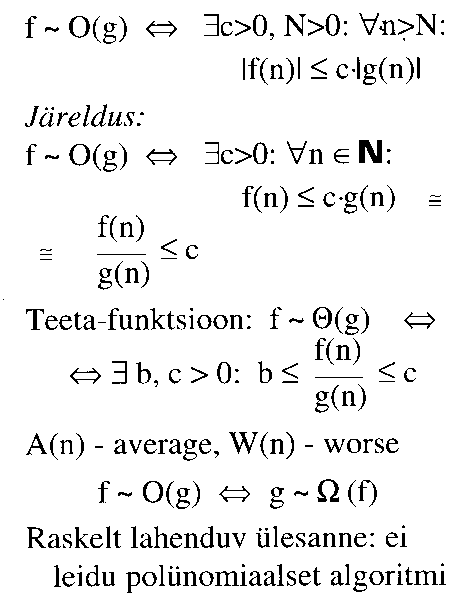
 Näide. Tõestame, et iga naturaalarvu k korral
nk ~ o(2n)
Näide. Tõestame, et iga naturaalarvu k korral
nk ~ o(2n).
Esmalt paneme tähele, et iga k jaoks leidub koht N, millest alates
kehtib:
n>N => n/k > log n [mat.
analüüsist: n kasvamisel lim (log n / n) = 0].
Siit
n > k log n ning veelgi enam
n +
log c > k log n = log nk.
Potentseerides saame
2nc > nk
ehk iga c>0 ja k jaoks leidub koht, millest alates
nk
< c2n m.o.t.t.
Complexity, average vs.
worst case, running time vs. memory space. Orders of growth:
definitions of "big-O", "small-o", "theta", "big-Omega" and
"small omega". Polynomial vs. exponential. Complexity classes:
constant, logarithmic, linear, nlogn, quadratic, cubic,
polynomial, exponential, factorial, ... Ackermann function.
Properties of asymptotic estimates.
Wikipedia
J. Pöial