Trees, representation of trees, traversal of trees

Definitions: nodes, parent-child relationship, root, leaves, external and internal nodes, ordered trees. Preorder traversal, postorder traversal. Binary trees, in-order traversal.
Arithmetic expression tree. Representation of trees: textual (left parenthetic and right parenthetic expressions, indented text, composite names), pointer structures. Implementation and examples.

Puu, puu esitusviisid ja töötlemine Javas

Puu (programmeerimisalal tavaliselt järjestatud puu):


Näide:  aritmeetilise avaldise puu

Aritmeetilise avaldise puu  



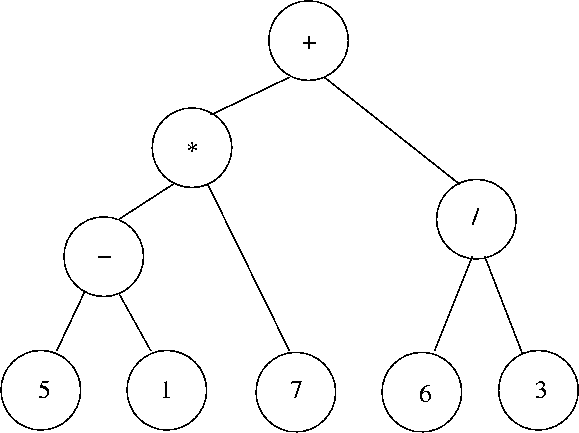
Infikskuju prioriteedisulgudega:  (5 - 1) * 7 + 6 / 3

Prefikskuju sulgudega:  + (* (- (5, 1), 7), / (6, 3))

Postfikskuju sulgudega:  (((5, 1)-, 7)*, (6, 3)/ )+

Pööratud poola kuju:  5 1 - 7 * 6 3 / +


Puu läbimine

Eesjärjestus (pre-order):

  1. Töödelda juur
  2. Töödelda juure alampuud järjestuses vasakult paremale

Lõppjärjestus (post-order, end-order):

  1. Töödelda juure alampuud järjestuses vasakult paremale
  2. Töödelda juur
Kahendpuu läbimine keskjärjestuses (in-order)
  1. Töödelda vasak alampuu
  2. Töödelda juur
  3. Töödelda parem alampuu

Avaldise prefikskuju saadakse puu läbimisega eesjärjestuses, postfikskuju (ja pööratud poola kuju) puu läbimisega lõppjärjestuses; läbimine keskjärjestuses ei anna praegusel juhul üheselt taastatavat avaldist!



Puu


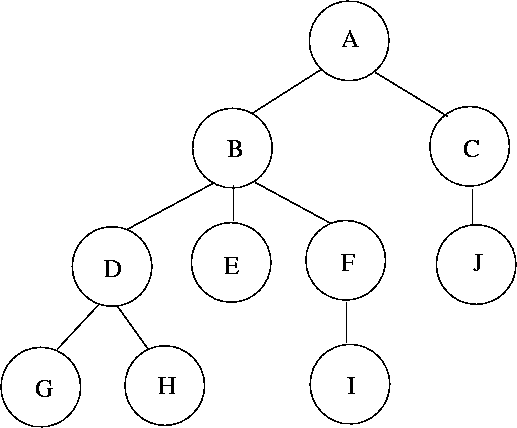
Preorder: A B D G H E F I C J

Postorder: G H D E I F B J C A


Puu esitusviisid

Graafiline (joonisena)

Vasakpoolne suluesitus

A(B(D(G,H),E,F(I)),C(J))

Parempoolne suluesitus

(((G,H)D,E,(I)F)B,(J)C)A

Tekstiline "treppimine"


A

B

D
G

H
E

F
I
C
J

Tippudele viitamine liitnimedega

A, A.B, A.C, A.B.D, A.B.E, A.B.F, A.B.D.G, A.B.D.H, A.B.F.I, A.C.J

Mittejärjestatud puu esitamiseks sobivad ka graafi esitusviisid (vajadusel fikseerida juurtipp) - näit. külgnevusmaatriks vms.

Puu esitusviisid töötlemiseks arvutis sõltuvad lahendatavast ülesandest - universaalset "parimat" kujutusviisi ei leidu:

Puu kujutamine ahelate abil

         Joonis  

Mõned puudega seotud ülesanded


Puu kujutamine Javas

Valime variandi, milles puu tipp sisaldab vahetute alluvate ahela algust ning viita järgmisele parempoolsele naabrile. Ülesliikumised korraldame magasini/rekursiooni abil.


import java.util.*;

public class TreeNode {

   private String name;
   private TreeNode rightSibling;
   private TreeNode firstChild;
   private int info;

   TreeNode (String s, TreeNode p, TreeNode a) {
      setName (s);
      setRightSibling (p);
      setFirstChild (a);
   }

   TreeNode (String s, TreeNode p, TreeNode a, int i) {
      setName (s);
      setRightSibling (p);
      setFirstChild (a);
      setInfo (i);
   }

   TreeNode() {
      this ("", null, null, 0);
   }

   TreeNode (String s) {
      this (s, null, null, 0);
   }

   TreeNode (String s, TreeNode p) {
      this (s, p, null, 0);
   }

   public void setName(String s) {
      name = s;
   }

   public String getName() {
      return name;
   }

   public void setRightSibling (TreeNode p) {
      rightSibling = p;
   }

   public TreeNode getRightSibling() {
      return rightSibling;
   }

   public void setFirstChild (TreeNode a) {
      firstChild = a;
   }

   public TreeNode getFirstChild() {
      return firstChild;
   }

   public void setInfo (int i) {
      info = i;
   }

   public int getInfo() {
      return info;
   }

   @Override
   public String toString() {
      return getName();  // TODO!!!
   }

   public void processTreeNode() {
      System.out.print (getName() + " ");
   }

   public void addChild (TreeNode a) {
      if (a == null)
         throw new IllegalArgumentException ("cannot add child null");
      TreeNode ptr = getFirstChild();
      if (ptr == null)
         setFirstChild (a);
      else {
         ptr = getFirstChild();
         while (ptr.getRightSibling() != null) {
            ptr = ptr.getRightSibling();
         }
         ptr.setRightSibling (a);
      }
   }

   public boolean isLeaf() {
      return (getFirstChild() == null);
   }

   public int size() {
      int n = 1; // root
      TreeNode ptr = getFirstChild();
      while (ptr != null) {
         n = n + ptr.size();
         ptr = ptr.getRightSibling();
      }
      return n;
   }

   public void preorder() {
      processTreeNode();
      TreeNode ptr = getFirstChild();
      while (ptr != null) {
         ptr.preorder();
         ptr = ptr.getRightSibling();
      }
   }

   public void postorder() {
      TreeNode ptr = getFirstChild();
      while (ptr != null) {
         ptr.postorder();
         ptr = ptr.getRightSibling();
      }
      processTreeNode();
   }

   public static TreeNode createTree() {
      TreeNode root = new TreeNode ("+", null,
         new TreeNode ("*",
            new TreeNode ("/", null,
               new TreeNode ("6",
                  new TreeNode ("3", null, null),
                  null)),
            new TreeNode ("-",
               new TreeNode ("4", null, null),
               new TreeNode ("2",
                  new TreeNode ("1", null, null),
                  null))));
      return root;
   }

   public static void main (String[] param) {
      TreeNode t = createTree();
      System.out.println ("Number of nodes: " + String.valueOf (t.size()));
      System.out.print ("Preorder:  ");
      t.preorder();
      System.out.println();
      System.out.print ("Postorder: ");
      t.postorder();
      System.out.println();
   }

}

Jaanus Pöial