3. praktikum

1. Poes müüakse 3 sorti piima. Ühe liitri hind on ühel sordil 7.90, teisel 8.10 ja kolmandal 8.15. Kaarel valib poes käies esimest sorti piima tõenäosusega 50%, teist tõenäosusega 10% ja kolmandat tõenäosusega 40% . Kui palju maksab ta keskmiselt piimaliitri eest?

Vastus: EX = 8,02

2. 10000 loteriipileti kohta on 1000-krooniseid võite 1, 100-krooniseid 12 ja 10-krooniseid 100. Milline peaks olema loteriipileti minimaalne hind, et korraldajatel poleks keskmise sissetuleku ja väljamineku mõttes ohtu kahjumisse jääda?

Vastus: 32 senti (ümardatult 35 senti)

3. Juhuslik suurus on ühtlase jaotusega lõigul [1; 3]: X ~ U(1; 3). Kirjutada välja tema tihedus- ja jaotusfunktsioon. Leida tema keskväärtus ja dispersioon.

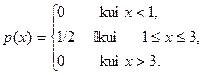
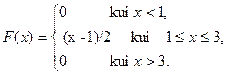EX = 2, DX = 1/3

4. Katseklaasis on 100000 bakterit. Sekundi jooksul sureb bakter tõenäosusega 0,00004. Missugune on tõenäosus, et sekundi jooksul sureb 0, 1, 2, …, 20 bakterit? Mitte üle 25 bakteri?
Vastus: P(X=0) = 0,018316; P(X=1) = 0,073263; P(X=2) = 0,146525; … P(X£25) = 1

5. Nõudlus teatud tüüpi kassettmagnetofoni järgi kaupluses on Poissoni jaotusega juhuslik suurus parameetriga l = 2.0. Leida tõenäosus selleks, et päevas ei müüda üle 4 magnetofoni.

Vastus: P(X£4) = 0,947

6. Telefonikeskjaama saabub tunni jooksul keskmiselt 30 väljakutset. Leida tõenäosus selleks, et minuti jooksul ei saabu üle 2 väljakutse.

Vastus: P(X£2) = 0,9856

7. Tehas suunas lattu 500 kvaliteetset toodet. Tõenäosus selleks, et transportimisel toodet vigastatakse, on 0,002. Leida, millise tõenäosusega saabub lattu 3 vigastatud toodet.

Vastus: P(X=3) = 0,0613

8. Valgusfoori töötsükli pikkus kui juhuslik suurus allub ühtlasele jaotusele keskväärtuega 45 sekundit. Pikima ja lühima tsükli vahe on 4 sekundit. Arvutada selle jaotuse standardhälve. Kui suur on tõenäosus, et tsükli pikkus on vähemalt 44 sekundit?
Vastus. s(X) = 1,15; P(44 < X < 47) = 0,75.

9. Auto tehnilise hoolduse aeg allub eksponentjaotusele. Ühe sõiduki teenindamisele kulub keskmiselt 2 tundi. Leida tõenäosus, et ühe auto teenindusaeg on 1) alla ühe tuni; 2) üle kolme tunni.
Vastus. 1) 0,39; 2) 0,22.

10. Arvutada P(0 £ X £ 1) ja P(|X - m| < 0,1), kui juhusliku suurue X jaotus on normaalne ning keskväärtus m = 1,4 ja dispersioon DX = 3,24.
Vastus. 1) 0,1937; 2) 0,0443.

11. Normaaljaotusega juhusliku suuruse keskväärtus on 40 ja dispersioon 200. Kui suur on tõenäosus, et
1) juhusliku suuruse mõõdetav väärtus on vahemikus (30; 80);
2) juhusliku suuruse kolmest sõltumatust väärtusest ükski ei oleks vahemikus (30; 80).
Vastus. 1) 0,758; 2) 0,01419.

12. Teatud automudeli läbisõit allub normaaljaotusele keskväärtusega 160000 km ja standardhälbega 30000 km. Kui suur on tõenäosus, et ostetud auto läbisõit on piirides 100000 km kuni 180000 km.
Vastus. 0,725

13. Kui suur on tõenäosus, et sajast istutatud puust läheb kasvama 65 kuni 75, kui ühe puu kasvamaminemise tõenäosus on 0,7?
Vastus. Täpne väärtus: 0,7704. Ligikaudne väärtus Laplace’i integraalse piirteoreemi kohaselt: 0,767

14. Vaatlused on näidanud, et 30% kauplusekülastajatest sooritab ostu. Päevas külastab kauplust keskmiselt 110 inimest. Kui suur on tõenäosus, et konkreetsel päeval on ostjaid 1) vähemalt 30; 2) alla 40?
Vastus. 1) Täpne väärtus: 0,76; ligikaudne väärtus 0,73 2) Täpne väärtus: 0,91 ; ligikaudne väärtus: 0,89

15. Märki tabamise tõenäosus ühel lasul on 0,8. Kui tõenäone on, et sajast lasust tabatakse 75 korral?
Vastus. Täpne väärtus: 0,044; Ligikaudne väärtus: 0,046